4.3 Regionales Modell |
Beim regionalen Modell (auch als Migrationsmodell oder feinkörniges Modell bezeichnet) erfolgt eine Beschränkung der Selektion auf voneinander getrennte Teile der Population. Dadurch erfolgt eine Unterteilung der Gesamtpopulation in einzelne Unterpopulationen. Diese Unterpopulationen entwickeln sich unabhängig voneinander. In jeder Unterpopulation läuft ein eigener Evolutionärer Algorithmus. Die Fitneßberechnung und Selektion, die sonst in der Gesamtpopulation zwischen allen Individuen stattfindet, wird beim regionalen Modell nur zwischen den Individuen der jeweiligen Unterpopulation durchgeführt; es findet eine regionale Fitneßberechnung und Selektion statt.
Diese durch die Reichweite der Selektion hervorgerufene Unterteilung der Population wird aber nicht über alle Generationen aufrecht erhalten. Von Zeit zu Zeit wird ein Austausch von Informationen zwischen den Unterpopulationen durchgeführt. Die Art und Weise sowie der Umfang der ausgetauschten Informationen haben einen großen Einfluß auf die Arbeitsweise des regionalen Modells.
Solange kein Austausch von Informationen stattfindet, entwickeln sich die Unterpopulationen unabhängig voneinander. Dies geschieht über eine Reihe von Generationen und wird als Isolationszeit bezeichnet. Nach dieser Isolationszeit findet der Austausch von Informationen durch den Austausch von Individuen zwischen den Unterpopulationen statt. Dieser Vorgang wird als Migration bezeichnet. Nach der Migration entwickeln sich die Unterpopulationen wieder unabhängig voneinander, bis es nach Ablauf der Isolationszeit wieder zu einer Migration von Individuen kommt.
Durch das regionale Modell wird eine direkte Unterteilung der Population eingeführt. Diese ist durch folgende Parameter gekennzeichnet:
Durch diese beiden Größen ist gleichzeitig die Gesamtzahl der Individuen der Population definiert.
Zusätzlich zu den bisherigen Operatoren Evolutionärer Algorithmen wird durch das regionale Modell der neue Operator Migration eingeführt. Der Migrationsoperator wird durch die folgenden Parameter bestimmt:
Durch die Wahl dieser Parameter kann beeinflußt werden, wieviele Informationen zwischen den Unterpopulationen ausgetauscht werden und wie schnell sich Informationen in der gesamten Population ausbreiten können. Damit wird beeinflußt, ob sich die Unterpopulationen eher unabhängig voneinander entwickeln oder ob sie sich ähnlich wie eine große Gesamtpopulation verhalten.
Durch eine Unterteilung der Population und einen nicht zu hohen Austausch von Informationen ist es möglich, die Verschiedenartigkeit der Individuen in einer Population länger zu erhalten, als dies mit einer vergleichbaren Gesamtpopulation möglich wäre. In einer einheitlichen (panmictic) Population werden die Individuen nach jeder Generation untereinander ähnlicher. Dieser Effekt wird durch die genetische Drift (siehe auch Selektionsvarianz bei der Erläuterung der einzelnen Selektionsverfahren, Abschnitt 3.2, ab S.) hervorgerufen. Dies führt zu einem zunehmenden Nachlassen der Effektivität des Rekombinationsoperators. Im Gegensatz zur einheitlichen Population entwickeln sich bei einer Unterteilung der Population die voneinander getrennten Bereiche mehr oder weniger unabhängig voneinander. Die Individuen werden durch die genetische Drift insgesamt weniger beeinflußt, da unter den Unterpopulationen die Verschiedenartigkeit länger erhalten bleibt. Dies hat außerdem eine bessere Erkundung unterschiedlicher Bereiche des Suchraumes zur Folge.
Ein Äquivalent für das regionale Modell findet sich in der natürlichen Evolution problemlos. So tendieren Arten dazu, sich in Untergruppen oder Unterpopulationen fortzupflanzen. Diese Unterpopulationen sind voneinander geographisch oder durch andere Schranken (kulturell, ökonomisch) lose oder stark getrennt. Nur von Zeit zu Zeit wandern einzelne Individuen von einer Unterpopulation zu einer anderen und pflanzen sich in der neuen Unterpopulation fort. Es ist wesentlich wahrscheinlicher, daß sich Individuen innerhalb ihrer Unterpopulation fortpflanzen, als daß dies zwischen Individuen verschiedener Unterpopulationen geschieht.
4.3.1 Anzahl und Größe der Unterpopulationen |
Die Anzahl und die Größe der Unterpopulationen, AnzUnterPop und AnzIndUnterPop, und damit die Gesamtzahl der zu verwendenden Individuen, sind stark von der Problemstellung abhängig und können allgemein nicht festgelegt werden. Im Verlauf der Arbeiten mit Evolutionären Algorithmen erwiesen sich einige Richtwerte als gute Startwerte für viele Probleme.
Als Grundlage für die Berechnung dient die Größe des Problems, die hier als Anzahl der Variablen der Zielfunktion definiert ist. Damit ist die wirkliche Anzahl der Problemvariablen gemeint (und nicht etwa die Anzahl der Variablen, die bei der Arbeit mit einer binären Repräsentation des Evolutionären Algorithmus für ein Problem mit reellen oder ganzzahligen Variablen benutzt werden).
Anzahl der Unterpopulationen:
Anzahl der Individuen pro Unterpopulation:
Die von diesen Überschlagsformeln gelieferten Werte, siehe Tabelle 4-1, sind Richtwerte, die eine obere Schranke darstellen. Mit diesen Werten wird eine relativ robuste Arbeit des Evolutionären Algorithmus gewährleistet. Sobald das Problem etwas genauer untersucht, problemspezifisches Wissen eingearbeitet und verschiedene Läufe durchgeführt wurden, können die Anzahl der Unterpopulationen sowie die Individuenzahl meist etwas niedriger gewählt werden als die von Gleichung 4-1 und 4-2 gelieferten Werte.
Wenn das regionale Modell auf einer parallelen Rechnerarchitektur implementiert wird, ist die Anzahl der Unterpopulationen durch die Anzahl der zur Verfügung stehenden Prozessoren vorgegeben bzw. die Anzahl der Unterpopulationen muß ein Vielfaches der Prozessorzahl sein. In Anlehnung an die oben gegebenen Richtwerte kann dann die Anzahl der Individuen pro Unterpopulation gewählt werden.
Variablen |
Unterpopulationen |
Individuen je Unterpopulation |
Gesamtzahl Individuen |
10 |
3 |
20 |
60 |
20 |
4 |
20 |
80 |
40 |
6 |
20 |
120 |
50 |
7 |
25 |
175 |
80 |
8 |
25 |
200 |
100 |
10 |
30 |
300 |
150 |
12 |
35 |
420 |
200 |
14 |
40 |
560 |
Tabelle 4-1: Anzahl der Unterpopulationen und Individuen je Unterpopulation sowie Gesamtzahl der Individuen in Abhängigkeit der Anzahl der Variablen des Problems
4.3.2 Migrationstopologien |
Mit der Migrationstopologie werden die Verbindungen zwischen den Unterpopulationen definiert. Nur auf diesen Verbindungen können Individuen von einer Unterpopulation zu einer anderen wandern. Für die Topologie gibt es viele verschiedene Möglichkeiten.
Migration kann stattfinden, z.B.:
Die allgemeinste Topologie ist die uneingeschränkte Migration (u.a. [PLG87]), siehe Abbildung 4-3. In diesem Fall ist jede Unterpopulation mit jeder anderen Unterpopulation verbunden. Daher wird dies auch als vollständige Netztopologie bezeichnet. Die Individuen, die in eine Unterpopulation wandern, können von jeder anderen Unterpopulation kommen. Der Ablauf einer solchen Migration ist in Abbildung 4-7 dargestellt.
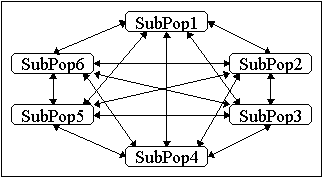
Abbildung 4-3: Struktur für die uneingeschränkte Migration (vollständige Netztopologie)
Das einfachste Schema ist die Migration in einer Ringtopologie (u.a. [GW91], [VBS91]), siehe Abbildung 4-4. Die Migranten können hier nur von den in einer Richtung benachbarten Unterpopulationen aus einwandern. In dem in Abbildung 4-4 links gegebenen Beispiel einer eindimensionalen Ringtopologie bedeutet dies, daß Individuen von Unterpopulation 6 zu Unterpopulation 1, Individuen von Unterpopulation 1 zu Unterpopulation 2 usw. wandern.
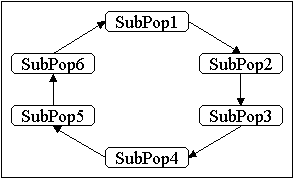
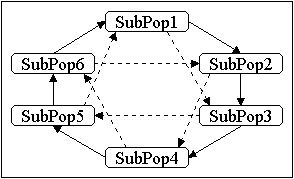
Abbildung 4-4: Migration in einer eindimensionalen Ringtopologie; links: Abstand 1, rechts: Abstand 1 und 2
Eine Erweiterung der Ringtopologie ist auf zwei Arten möglich. Zum Ersten kann der Abstand zu möglichen Nachbarn vergrößert werden. Ein Beispiel dafür ist in Abbildung 4-4 rechts gezeigt, hier bestehen auch Verbindungen zu Unterpopulationen, die den Abstand 2 haben. Bei einer Vergrößerung des Abstandes bis auf AnzUnterPop -1 geht die Ringtopologie in die vollständige Netztopologie über. Weiterhin kann die Ringtopologie in höhere Dimensionen übertragen werden. Bei der folgenden Erläuterung der Nachbarschaftstopologie wird darauf näher eingegangen.
Die Nachbarschaftstopologie ist der Ringtopologie ähnlich. Hierbei erfolgt eine Migration von Individuen von allen Nachbarn einer Unterpopulation aus. Der Abstand kann dabei auch höher als 1 gewählt werden. Eine eindimensionale Nachbarschaftstopologie geht bei einem Abstand von (AnzUnterPop -1)/2 in die vollständige Netztopologie über, für höherdimensionale Nachbarschaftstopologien ist dieser Wert noch kleiner. Abbildung 4-5 zeigt eine zweidimensionale Nachbarschaftstopologie mit Abstand 1. Diese Topologie wird auch als zweidimensionales Gitter bzw. als Torus bezeichnet. Für höhere Dimensionen ergibt sich ein Hyperwürfel (u.a. [Tan87], [Tan89], [CMR91], [VBS91]).
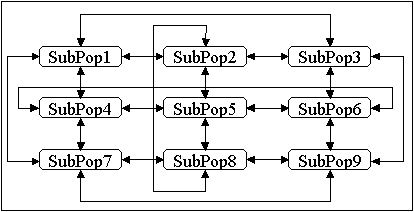
Abbildung 4-5: Migration in einer Nachbarschaftstopologie (2-D Gitter)
Eine Variante der zweidimensionalen Nachbarschaftstopologie stellt die Leitertopologie dar ([MSB91]), Abbildung 4-6. Bei gleicher Anzahl von Unterpopulationen besitzt diese Topologie einen größeren Durchmesser als eine zweidimensionale Gittertopologie, wodurch Informationen zwischen den Unterpopulationen deutlich langsamer ausgetauscht werden.
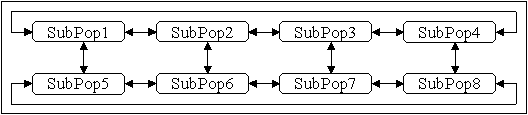
Abbildung 4-6: Migration in einer zweidimensionalen Leitertopologie
Bei einer Implementierung des regionalen Modells auf einer parallelen Rechnerarchitektur ist die Topologie der Unterpopulationen meist durch die Topologie des entsprechenden Rechnersystems gegeben. Oftmals ist dies ein zweidimensionales Gitter (2-D Implementierung der Nachbarschaftstopologie) oder ein Hyperwürfel. Auf transputerbasierten Systemen ist dagegen meist nur die maximale Anzahl von Nachbarn vorgegeben, wodurch sehr unterschiedliche Topologien realisiert werden können.
Ein Vergleich der verschiedenen Topologien für die Migration ist nicht ganz einfach. Die entscheidende Frage ist ein Vergleichskriterium, nach dem die Topologien untereinander verglichen werden können. Die Anzahl der Nachbarn einer Unterpopulation im Verhältnis zur Gesamtzahl aller Unterpopulationen, der Durchmesser der Topologie, der Abstand von einer Unterpopulation zur jeweils am weitesten entfernten Unterpopulation und die mögliche Geschwindigkeit des Informationsflusses könnten zusammen ein Kriterium ergeben. Bei der Beschreibung des lokalen Modells (Abschnitt 4.4, ab S.) wird nochmals auf die Definition von Nachbarschaften und Topologien eingegangen. Im Unterabschnitt 4.4.2, S., wird eine allgemeinere Beschreibung von Nachbarschaften gegeben, die einen Vergleich der einzelnen Topologien erleichtert.
4.3.3 Migrationsintervall und Migrationsrate |
Migrationsintervall und Migrationsrate steuern den Austausch von Individuen zwischen den Unterpopulationen. Das Migrationsintervall gibt an, wie oft bzw. wann Migration stattfindet. Die Migrationsrate gibt den Anteil oder die Anzahl der Individuen einer Unterpopulation an, die ausgetauscht werden. Beide Parameter zusammengenommen geben die Menge an Information an, die durch Migration zwischen den Unterpopulationen ausgetauscht werden soll.
Das Migrationsintervall kann als eine fest definierte Zahl von Generationen gegeben sein und definiert damit die Isolationszeit (die Zeit, in der sich die Unterpopulationen isoliert voneinander entwickeln). Der Wert kann zwischen 1 und einer größeren Zahl von Generationen gewählt werden. Bei kleineren Unterpopulationen sollte das Migrationsintervall kleiner sein als bei Verwendung größerer Unterpopulationen (Abhängigkeit des Migrationszeitpunktes von der Anzahl der Individuen in den Unterpopulationen, AnzIndUnterPop). Der Zeitpunkt für eine Migration kann aber auch in Abhängigkeit von anderen Ereignissen als der Zahl vergangener Generationen definiert werden. Eine Variante ist die vorzeitig auftretende Konvergenz bei Unterpopulationen. Eine weitere Möglichkeit besteht darin, immer dann eine Migration durchzuführen, wenn in einer Unterpopulation ein besseres Individuum gefunden wurde.
Die Migrationsrate wird als Anteil der Unterpopulation oder als feste Zahl von Individuen pro Unterpopulation angegeben, wobei die erste Angabe über verschiedene Unterpopulationsgrößen vergleichbar ist und deshalb hier verwendet wird. Die Migrationsrate sollte immer nur einen Teil der Unterpopulation umfassen. In verschiedenen Arbeiten mit Evolutionären Algorithmen haben sich folgende Richtwerte als gute Startwerte erwiesen.
Migrationsintervall:
![]() (4-3)
(4-3)
Migrationsrate:
![]() (4-4)
(4-4)
Bei einem sehr kleinen Wert für das Migrationsintervall (< 10 Generationen), sollte die Migrationsrate auch sehr klein sein, da sonst zuviel Information zwischen den Unterpopulationen ausgetauscht wird. Bei einem Migrationsintervall von einer Generation (häufigste Migration) wird meist eine Migrationsrate von einem Individuum (minimale Migrationsrate) gewählt ([PLG87]).
Wenn die Migrationsrate groß und/oder das Migrationsintervall klein gewählt werden, verhält sich das regionale Modell ähnlich dem globalen Modell, da kaum noch eine Isolation zwischen den Unterpopulationen besteht.
4.3.4 Auswahl der Migranten |
Während der Migration findet an zwei Stellen eine Selektion von Individuen statt. Zuerst werden die Individuen ausgewählt, die aus einer Unterpopulation auswandern (Migrationsauswahl). Danach müssen die Individuen ausgewählt werden, die in der Unterpopulation durch die eingewanderten Individuen (Migranten) ersetzt werden sollen (Migrationsauslese).
Für die Auswahl der Individuen gibt es verschiedene Kombinationen:
Wenn eine fitneßproportionale Auswahl verwendet wird, so übt die Migration einen zusätzlichen Selektionsdruck in Richtung der besseren Individuen aus. Bei der zufällig - zufällig erfolgenden Auswahl dagegen findet nur ein Durchmischen der Individuen zwischen den Unterpopulationen statt, es wird kein zusätzlicher Selektionsdruck ausgeübt.
4.3.5 Ablauf der Migration |
Abbildung 4-7 zeigt den Ablauf der Migration von Individuen zwischen Unterpopulationen. In diesem Beispiel werden vier Unterpopulationen, die vollständige Netztopologie (uneingeschränkte Migration), fitneßbasierte Auswahl der Migranten und eine Migrationsrate von einem Individuum verwendet. Das Beispiel zeigt, wie Individuen in die Unterpopulation 1 wandern.
Zu Beginn werden die Unterpopulationen ausgewählt, die mit Unterpopulation 1 durch die verwendete Migrationstopologie verbunden sind. Durch die verwendete vollständige Netztopologie sind das in diesem Falle alle anderen Unterpopulationen 2, 3 und 4. Aus diesen Unterpopulationen werden jeweils entsprechend der Selektionsmethode (fitneßbasiert - Auswahl der besten Individuen) und der Migrationsrate (ein Individuum) Individuen als potentielle Migranten ausgewählt, im Beispiel das jeweils beste Individuum dieser Unterpopulationen. Diese Individuen bilden einen Pool, aus dem gleichmäßig zufällig das Individuum ausgewählt wird, das in Unterpopulation 1 eingefügt wird und dabei das schlechteste Individuum in Unterpopulation 1 ersetzt. Dieser Ablauf wird für jede Unterpopulation durchgeführt. Durch dieses Verfahren ist gleichzeitig sichergestellt, daß keine Unterpopulation Individuen von sich selbst erhält.
Bei einer anderen Topologie für die Migration ändern sich nur die Unterpopulationen, aus denen die Individuen für die Migration in eine bestimmte Unterpopulation ausgewählt werden. Der Ablauf ist ansonsten identisch.
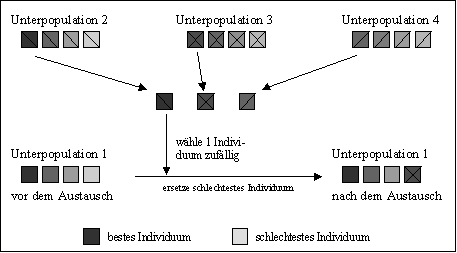
Abbildung 4-7: Ablauf der Migration von Individuen zwischen Unterpopulationen
4.3.6 Analyse des regionalen Modells |
Die parallele Implementierung des regionalen Modells brachte nicht nur eine Beschleunigung der Berechnungszeiten. Es zeigte sich, daß bei einer Vielzahl untersuchter Zielfunktionen weniger Zielfunktionsberechnungen zum Erreichen eines gleichwertigen Ergebnisses benötigt wurden, als bei Verwendung einer Gesamtpopulation mit entsprechend vielen Individuen. Gleichlautende Ergebnisse wurden bisher in vielen Untersuchungen berichtet, u.a. [Bel95], [GW91], [Loh91], [MSB91], [Rud91], [SWM91], [Swm96], [Tan89], [VBS91], [VSB92]. Damit ergibt sich, daß die Verwendung des regionalen Modells auch bei einer sequentiellen Implementierung (Computer mit einem Prozessor) Vorteile bringt. Der Evolutionäre Algorithmus findet öfter eine Lösung (robuster) oder die Lösung wird mit weniger Zielfunktionsberechnungen ermittelt (schneller).
Mühlenbein stellte fest:
,,Unterpopulationen, die für eine gewisse Zeit isoliert voneinander sind, halten die Verschiedenartigkeit der Population hoch. Nach der Migration von Individuen werden neue vielversprechende Bereiche durch Rekombination entdeckt." ([Müh91], S.323)
Wenn die von Individuen in unterschiedlichen Unterpopulationen gefundenen Teillösungen in ihrer Kombination (durch Rekombination) eine bessere Lösung ergeben, so sollte die Anwendung des regionalen Modells deutliche Vorteile gegenüber dem globalen Modell (oder einem einfachen Evolutionären Algorithmus) bringen. Erzeugt die Kombination der Teillösungen dagegen eine schlechtere Lösung, so müßte eine einheitliche Gesamtpopulation Vorteile haben [SWM91].
Aus diesen beiden Anmerkungen sind bereits die Einsatzgebiete des regionalen Modells vorgezeichnet. Die Unterpopulationen arbeiten meist (besonders zu Beginn eines Laufs) in unterschiedlichen Bereichen des Suchraumes. Dabei werden unterschiedliche Teillösungen gefunden. Wenn sich aus den Teillösungen der verschiedenen Unterpopulationen bessere Lösungen zusammensetzen lassen, so ist die Verwendung des regionalen Modells von Vorteil. Viele der oft genutzten Testfunktionen zur Demonstration der Vorteile des Einsatzes des regionalen Modells sind meist so konstruiert, daß sich die Gesamtlösung durch Kombination von Einzellösungen ermitteln läßt (z.B. Rastrigin's Funktion, Griewangk's Funktion, Schwefel's Funktion, siehe [Poh96]).
Finden dagegen alle Unterpopulationen dieselbe Lösung bzw. benutzen denselben Weg durch den Suchraum, so arbeitet eine Gesamtpopulation effektiver. Wenn die Teillösungen der Unterpopulationen in ihrer Kombination schlechtere Lösungen ergeben, so ist die Migration von Individuen im regionalen Modell von Nachteil. In diesem Falle verbliebe nur der Vorteil der Suche in unterschiedlichen Bereichen des Suchraumes und das langsamere Absinken der Diversität der Individuen in der Gesamtpopulation.
Diese Dokument ist Teil der Dissertation von Hartmut Pohlheim
"Entwicklung und systemtechnische Anwendung Evolutionärer Algorithmen".
This document is part of the .
The is not free.
© Hartmut Pohlheim, All Rights Reserved,
(hartmut@pohlheim.com).