3.2 Selektion |
Durch die Selektion werden die Individuen zur Produktion von Nachkommen ausgewählt. Im ersten Schritt wird jedem Individuum der Population eine Fitneß zugewiesen. Diese Fitneß entspricht der Fortpflanzungswahrscheinlichkeit (und damit der Selektionswahrscheinlichkeit) und hängt vom Zielfunktionswert dieses Individuums und den Zielfunktionswerten aller anderen Individuen des entsprechenden Selektionspools ab. Die Fitneß wird im folgenden Schritt, der aktuellen Auswahl der Individuen, verwendet.
Innerhalb dieses Abschnitts werden einige Begriffe zum Vergleich der einzelnen Verfahren benutzt. Eine Erläuterung dieser Begriffe, die sich an [Bak87] und [BT95] orientiert, wird hier vorangestellt:
Selektionsdruck (selective pressure)
· Wahrscheinlichkeit der Auswahl des besten Individuums, verglichen mit der durchschnittlichen Selektionswahrscheinlichkeit aller Individuen des Selektionspools,
bias
· absolute Differenz zwischen der normalisierten Fitneß eines Individuums und seiner erwarteten Reproduktionswahrscheinlichkeit,
spread
· Bereich der möglichen Werte für die Anzahl der Nachkommen eines Individuums,
Loss of diversity (Verlust an Vielfalt/Mannigfaltigkeit/Diversität)
· Anteil der Individuen des Selektionspools, die während einer Selektionsphase nicht ausgewählt werden (die Individuen/Informationen, die bei einer vollständigen Ersetzung der Elternpopulation durch die Nachkommenpopulation verloren gehen würden),
Selektionsintensität (selection intensity)
· erwarteter durchschnittlicher Fitneßwert der selektierten Individuen nach einer durchgeführten Selektion (Voraussetzung: normalverteilte Fitneßwerte des Selektionspools).
Selektionsvarianz (selection variance)
· erwartete Varianz der Fitneßwerte der selektierten Individuen nach einer durchgeführten Selektion (Voraussetzung: normalverteilte Fitneßwerte des Selektionspools).
3.2.1 Fitneßzuweisung |
Bei der Fitneßzuweisung wird jedem Individuum seine Fortpflanzungswahrscheinlichkeit (Fitneß) zugewiesen. Dieser Fitneßwert wird aus dem Zielfunktionswert des Individuums und den Zielfunktionswerten aller anderen Individuen des Selektionspools unter Verwendung einer Fitneßfunktion gebildet. Die Fitneßfunktion führt eine Transformation der Zielfunktionswerte in nichtnegative Werte durch.
Die Fitneß eines Individuums ist immer im Vergleich zu allen anderen Individuen des Selektionspools zu betrachten. (Im Gegensatz zum Zielfunktionswert, der nur von den Variablen des Individuums abhängt.)
Für die Fitneßzuweisung lassen sich drei Verfahren unterscheiden:
Bei der proportionalen Fitneßzuweisung wird jedem Individuum ein Fitneßwert zugewiesen, der proportional zu seinem Zielfunktionswert ist. Für die Fitneßfunktion wurden verschiedene Verfahren (u.a. [GB89]) verwendet. Die wichtigsten Skalierungen sind in Gleichung 3-1 dargestellt.
Bei der Verwendung dieser Fitneßfunktionen treten jedoch Probleme auf. Abbildung 3-3 dient zur Veranschaulichung zweier Beispiele, an denen sich diese Probleme deutlich zeigen.
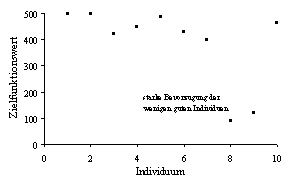
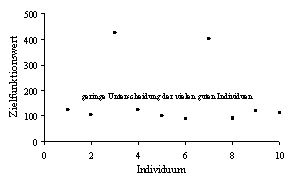
Abbildung 3-3: Probleme bei der Verwendung der proportionalen Fitneßzuweisung; links: die wenigen guten Individuen (Minimierung: ein kleinerer Zielfunktionswert ist besser) werden zu stark bevorzugt, rechts: die vielen guten Individuen unterscheiden sich untereinander kaum in ihrer Fitneß
Im linken Diagramm von Abbildung 3-3 sind eine Anzahl von Zielfunktionswerten dargestellt, wobei zwei Individuen einen sehr niedrigen Zielfunktionswert haben, alle anderen Individuen einen wesentlich höheren und in etwa gleichen Wert. Bei einer proportionalen Fitneßzuweisung würden die beiden guten Individuen eine sehr hohe Fitneß im Vergleich zu den schlechten Individuen zugewiesen bekommen. Dies hätte zur Folge, daß die wenigen guten Individuen sehr viele Nachkommen produzieren würden, von den schlechten Individuen würden nur wenige überhaupt eine Chance zur Produktion von Nachkommen bekommen. Die in der Population vorhandene Mannigfaltigkeit würde dadurch sehr schnell verloren gehen. Dieser Vorgang wird als vorzeitige Konvergenz (premature convergence) bezeichnet und hat seine Ursache im zu hohen Selektionsdruck, der durch die proportionale Fitneßzuweisung erzeugt wurde.
Im rechten Diagramm von Abbildung 3-3 sind Zielfunktionswerte dargestellt, bei denen viele ähnlich gute Individuen auftreten und nur wenige schlechte Individuen. In diesem Fall würde es bei der proportionalen Fitneßzuweisung zu einer sehr geringen Unterscheidung in den Fitneßwerten der guten Individuen kommen. Die Auswahl zwischen den guten Individuen würde eher einer zufälligen Auswahl gleichen. Dies wird als Steckenbleiben (stagnation) bezeichnet und durch den zu geringen Selektionsdruck hervorgerufen, der durch die proportionale Fitneßzuweisung erzeugt wurde.
Zusammenfassend kann festgestellt werden, daß durch die Fitneßzuweisung eine Verteilung der Fitneßwerte in der Art zu erfolgen hat, daß wenige gute Individuen keine übermäßige Anzahl von Nachkommen produzieren und bei vielen guten Individuen trotzdem eine signifikante Unterscheidung der Fitneßwerte der guten Individuen stattfindet.
Diese Aufgabe einer effektiven Kontrolle des Selektionsdruckes kann durch eine proportionale Fitneßzuweisung nicht allgemein gelöst werden. Für spezielle Anwendungen dagegen, bei denen die Verteilung der Zielfunktionswerte in etwa bekannt ist, kann die proportionale Fitneßzuweisung ausreichend sein.
Eine robuste Lösung bringt erst die reihenfolgebasierte Fitneßzuweisung. Die proportionale Fitneßzuweisung sollte heute, außer in Spezialfällen, nicht mehr verwendet werden und wird deshalb hier auch nicht weiter erläutert.
Bei der reihenfolgebasierten Fitneßzuweisung wird der Selektionspool entsprechend der Zielfunktionswerte sortiert. Die einem Individuum zugewiesene Fitneß hängt hier nur von der Position/dem Rang des Individuums in dieser sortierten Liste ab (und damit nicht vom Zielfunktionswert). Damit werden die oben besprochenen Probleme der proportionalen Fitneßzuweisung vermieden. Durch die reihenfolgebasierte Fitneßzuweisung wird eine gleichmäßige Skalierung über den Selektionspool eingeführt, die zu einem einfachen und effektiven Weg der Kontrolle der Verteilung der Fitneßwerte führt.
Für die Durchführung der Fitneßzuweisung werden folgende Variablen verwendet: Nind ist die Anzahl der Individuen im Selektionspool, Pos die Position/der Rang eines Individuums im sortierten Selektionspool (das schlechteste Individuum hat die Position Pos = 1, das beste Individuum die Position Pos = Nind), SP ist der Selektionsdruck.
Zwei Fitneßfunktionen werden vorgestellt: lineares und nichtlineares Ranking. Damit berechnet sich der Fitneßwert eines Individuums durch:
Lineares Ranking:
![]() (3-2)
(3-2)
Lineares Ranking erlaubt einen Selektionsdruck im Bereich [1.0, 2.0].
In [Poh95] wurde eine Methode des Ranking unter Verwendung einer nichtlinearen Verteilung eingeführt, welche die direkte Angabe des gewünschten Selektionsdrucks erlaubt. Die Benutzung des nichtlinearen Ranking erlaubt die Verwendung eines höheren Selektionsdruckes, als dies beim linearen Ranking möglich ist.
Nichtlineares Ranking:
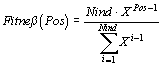 (3-3)
(3-3)
X kann bei Angabe des Selektionsdruckes SP und der Individuenzahl Nind direkt als Lösung des folgenden Polynoms berechnet werden:
![]() (3-4)
(3-4)
Nichtlineares Ranking erlaubt einen Selektionsdruck im Bereich [1.0, Nind - 2.0].
In Abbildung 3-4 werden lineares und nichtlineares Ranking grafisch miteinander verglichen.
Die Wahrscheinlichkeit eines Individuums, ausgewählt zu werden, ergibt sich aus seiner Fitneß, normalisiert mit der gesamten Fitneß des Selektionspools. Bei dem hier angegebenen Verfahren ist die Fitneß gleich der Selektionswahrscheinlichkeit, da die Normalisierung schon innerhalb der Fitneßfunktion durchgeführt wurde.
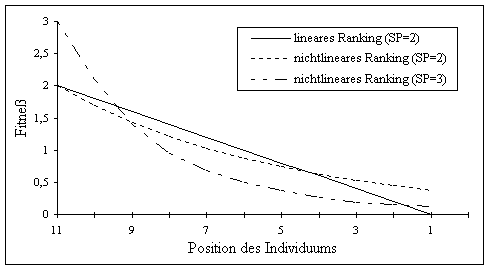
Abbildung 3-4: Vergleich der Fitneßfunktionen für lineares und nichtlineares Ranking
Das robuste Verhalten der reihenfolgebasierten Fitneßzuweisung wurde in einer Reihe von Arbeiten (u.a. [BH91], [Why89]) gezeigt und ist die Methode der Wahl für die Fitneßzuweisung.
3.2.2 Fitneßproportionale Selektion |
Bei der fitneßproportionalen Selektion werden die Individuen entsprechend ihrer Fitneß aus dem Selektionspool ausgewählt. Als Grundlage dient der absolute Fitneßwert. Die Rouletteselektion ist das bekannteste Verfahren, stochastic universal sampling dagegen das optimale Verfahren.
Das bekannteste Verfahren zur Auswahl von Individuen ist die Rouletteselektion, auch als stochastic sampling with replacement bezeichnet [Bak87]. Dies ist ein stochastisches Verfahren, das nach folgendem Prinzip funktioniert:
Die Individuen des Selektionspools werden einzelnen Abschnitten einer Linie zugeordnet. Die Größe eines jeden Abschnittes entspricht der Fitneß des Individuums. Jetzt wird eine Zufallszahl (gleichverteilt im Bereich zwischen null und Länge der Linie) generiert. Das Individuum, in dessen Abschnitt diese Zufallszahl zeigt, wird ausgewählt. Dieser Vorgang wird so oft wiederholt, wie Individuen ausgewählt werden sollen. Dies entspricht einem Roulette, nur daß hier die Größe der Abschnitte der Fitneß jedes Individuums entspricht.
Die Rouletteselektion hat einen bias von null. Es kann aber kein minimaler spread garantiert werden.
Stochastic universal sampling [Bak87] ist ähnlich der Rouletteselektion. Die Individuen des Selektionspools werden einzelnen Abschnitten einer Linie zugeordnet, genau wie bei der Rouletteselektion. Anders ist dagegen, daß hier eine Anzahl von Zeigern gleichmäßig über die Linie verteilt werden. Die Anzahl der Zeiger entspricht der Anzahl von Individuen NSelect, die auszuwählen sind. Der Abstand zwischen jeweils benachbarten Zeigern beträgt 1/NSelect. Diese Zeiger werden durch eine Zufallszahl im Bereich [0, 1/NSelect] vom Nullpunkt der Linie aus verschoben. Der erste Zeiger befindet sich damit an der Stelle der einen Zufallszahl, alle anderen Zeiger in gleichem Abstand 1/NSelect hinter dem ersten Zeiger.
Durch dieses Verfahren, das nur die Ziehung einer Zufallszahl beinhaltet, wird ein bias von null und ein minimaler spread garantiert. Stochastic universal sampling ist ein optimales Selektionsverfahren in Bezug auf bias und spread. Für die fitneßproportionale Selektion ist bis heute kein besseres (schnelleres) Verfahren gefunden worden. Damit ist stochastic universal sampling das Verfahren der Wahl für die fitneßproportionale Selektion.
In [BT95] wurde eine Analyse der fitneßproportionalen Selektion mit linearem Ranking als Fitneßzuweisung (lineare Ranking-Selektion) durchgeführt.
Selektionsintensität:
![]() (3-5)
(3-5)
Loss of diversity:
![]() (3-6)
(3-6)
Selektionsvarianz:
![]() (3-7)
(3-7)
Die Eigenschaften der linearen Ranking-Selektion sind in Abbildung 3-5 in Abhängigkeit des Parameters der linearen Ranking-Selektion, dem Selektionsdruck, grafisch veranschaulicht.
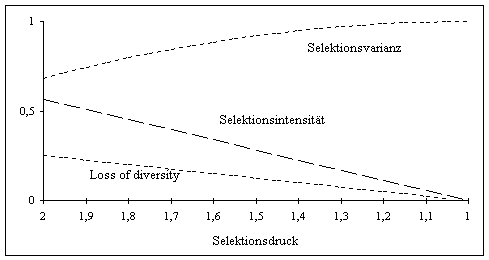
Abbildung 3-5: Eigenschaften der linearen Ranking-Selektion (fitneßproportionale Selektion mit linearem Ranking als Fitneßzuweisung)
3.2.3 Turnierselektion |
Bei der Turnierselektion [GD91] werden Turniere zwischen mehreren Individuen durchgeführt. Sieger eines Turniers und damit ausgewählt ist das jeweils beste Individuum (höchste Fitneß). Die Auswahl der Individuen, die an einem Turnier teilnehmen, wird gleichmäßig zufällig im Selektionspool durchgeführt. Die Anzahl der Individuen in einem Turnier, die Turniergröße Tour, ist der direkte Parameter der Turnierselektion. Die Turniergröße kann Werte von 1 (kein Selektionsdruck, da gleichmäßig zufällige Auswahl) bis zur Anzahl der Individuen im Selektionspool annehmen. Es werden so viele Turniere durchgeführt, wie Individuen auszuwählen sind.
Bei der Turnierselektion wird nur die Reihenfolge der Fitneßwerte der Individuen verwendet. Der absolute Wert der Fitneß wird nicht in Betracht gezogen. Deshalb kann für die Fitneßzuweisung jede Fitneßfunktion verwendet werden, solange sie eine monotone Zuweisung von Fitneßwerten entsprechend der Reihenfolge der Zielfunktionswerte vornimmt, siehe Gleichung 3-8.
Monotone Fitneßfunktion:
Alle im Unterabschnitt 3.2.1, ab S. angeführten Fitneßfunktionen erfüllen diese Forderung.
In [BT95] wurde eine Analyse der Turnierselektion durchgeführt.
Selektionsintensität (Approximation):
![]() (3-9)
(3-9)
Loss of diversity:
![]() (3-10)
(3-10)
Selektionsvarianz (Approximation):
![]() (3-11)
(3-11)
Diese Eigenschaften der Turnierselektion sind in Abbildung 3-6 in Abhängigkeit des Parameters der Turnierselektion, der Turniergröße, grafisch veranschaulicht.
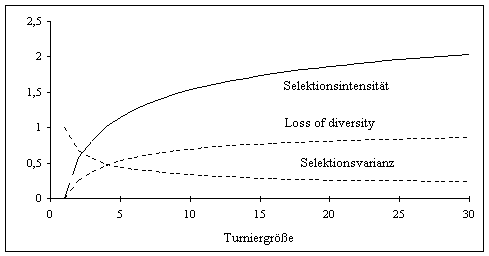
Abbildung 3-6: Eigenschaften der Turnierselektion
3.2.4 Truncation-Selektion |
Bei der Truncation-Selektion werden nur die besten Individuen ausgewählt. Dazu werden die Individuen entsprechend ihrer Fitneß sortiert. Alle Individuen mit einer Fitneß, die größer als eine festgelegte Schwelle ist, werden ausgewählt. Die anderen Individuen werden verworfen, sie bekommen keine Chance zur Produktion von Nachkommen. Die Schwelle wird als Anteil der Individuen des Selektionspools definiert, die ausgewählt werden und heißt Truncation-Schwelle Trunc (Abschneideschwelle). In Abbildung 3-7 wird dieser Prozeß nochmals verdeutlicht. Entsprechend seinem Rang im sortierten Selektionspool erhält ein Individuum eine Selektionswahrscheinlichkeit von eins (beste Individuen) oder null (schlechte Individuen).
Auch bei der Truncation-Selektion wird, ähnlich zur Turnierselektion, nur die Reihenfolge der Fitneßwerte der Individuen verwendet. Der absolute Wert der Fitneß wird nicht in Betracht gezogen. Deshalb kann für die Fitneßzuweisung jede Fitneßfunktion verwendet werden, solange sie eine monotone Zuweisung von Fitneßwerten entsprechend der Reihenfolge der Zielfunktionswerte vornimmt, siehe Gleichung 3-8.
Im Vergleich zu den bisherigen Selektionsmethoden, die Prinzipien der natürlichen Selektion modellieren, ist die Truncation-Selektion ein künstliches Selektionsverfahren. Es wird vor allem von Züchtern für sehr große Populationen bzw. die Massenselektion angewendet.
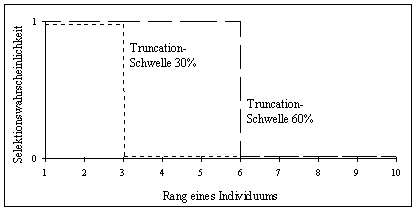
Abbildung 3-7: Prinzip der Truncation-Selektion: Selektionswahrscheinlichkeit eines Individuums in Abhängigkeit seines Ranges
In [BT95] wird eine Analyse der Truncation-Selektion durchgeführt. Dieselben Resultate wurden auf einem anderen Weg in [CK70] hergeleitet.
Selektionsintensität:
![]() (3-12)
(3-12)
Loss of diversity:
![]() (3-13)
(3-13)
Selektionsvarianz:
![]() (3-14)
(3-14)
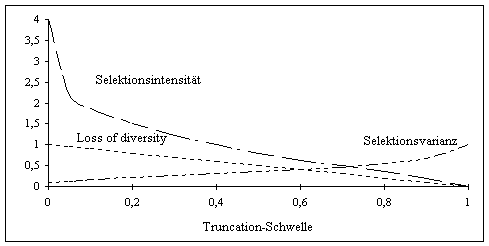
Abbildung 3-8: Eigenschaften der Truncation-Selektion
Diese Eigenschaften der Truncation-Selektion sind in Abbildung 3-8 in Abhängigkeit des Parameters der Truncation-Selektion, der Truncation-Schwelle, grafisch veranschaulicht.
3.2.5 Vergleich der Selektionsverfahren |
Der Vergleich der verschiedenen Selektionsverfahren aus [BT95] wurde bei der Beschreibung der einzelnen Verfahren schon mehrfach erwähnt. Hier sollen die Eigenschaften der verschiedenen Selektionsverfahren miteinander verglichen werden. Abschließend sollen daraus schlußfolgernd Hinweise zur Anwendung der Verfahren abgeleitet werden.
Die verschiedenen Selektionsverfahren können miteinander verglichen werden, wenn die verschiedenen Eigenschaften auf einen gemeinsamen Parameter zurückzuführen sind. Dazu bieten sich die Selektionsintensität und der Selektionsdruck an. In der Literatur wird die Selektionsintensität bevorzugt und deshalb auch hier genutzt.
In Abbildung 3-9 werden die jedem Selektionsverfahren eigenen Parameter (d.h. Selektionsdruck für lineare Ranking-Selektion, Truncation-Schwelle für Truncation-Selektion und Turniergröße für Turnierselektion) in Abhängigkeit von der Selektionsintensität dargestellt. Durch den bekannten Zusammenhang zwischen Selektionsintensität und Selektionsdruck könnte diese Abhängigkeit auch gegenüber dem Selektionsdruck für die verschiedenen Verfahren dargestellt werden. An dieser Stelle sei darauf hingewiesen, daß die Turnierselektion nur diskrete Werte zuläßt.
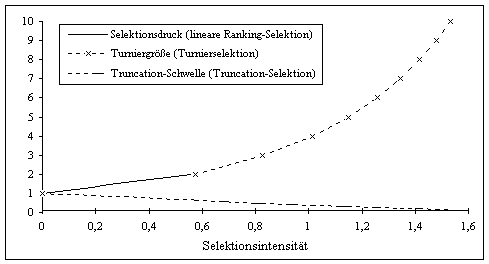
Abbildung 3-9: Abhängigkeit der Selektionsparameter von der Selektionsintensität
Obwohl die Parameter der Selektionsverfahren auf die gleiche Selektionsintensität zurückgeführt werden können, zeigen sich Unterschiede beim Vergleich der weiteren Eigenschaften der Verfahren. Die Abbildungen 3-10 und 3-11 vergleichen den Loss of diversity bzw. die Selektionsvarianz der Verfahren in Abhängigkeit von der Selektionsintensität.
Aus Abbildung 3-10 ist zu sehen, daß für ein und dieselbe Selektionsintensität bei der Truncation-Selektion ein höherer Loss of diversity auftritt, als dies bei der Turnierselektion und der linearen Ranking-Selektion der Fall ist. Bei der Truncation-Selektion ist die Wahrscheinlichkeit größer, daß nicht so gute Individuen durch bessere Individuen ersetzt werden, als dies bei den anderen Selektionsverfahren der Fall ist.
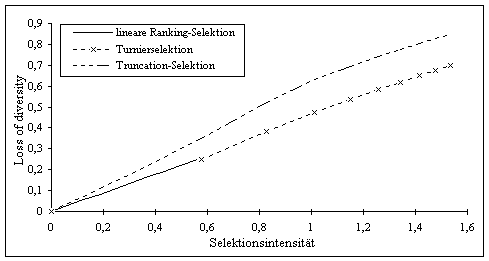
Abbildung 3-10: Abhängigkeit des Loss of diversity von der Selektionsintensität
Turnierselektion und lineare Ranking-Selektion sind in ihrem Verhalten bezüglich des Loss of diversity ähnlich zueinander. An den Randpunkten des Definitionsbereiches der linearen Ranking-Selektion sind beide Verfahren gleich. Für die anderen Bereiche ist jeweils nur eines der Verfahren definiert (komplementäres Verhalten beider Verfahren).
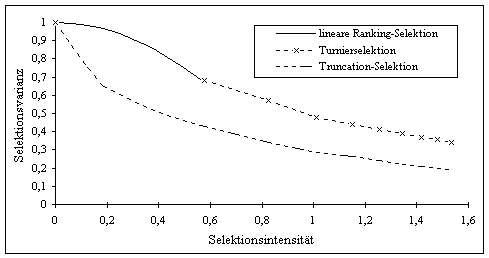
Abbildung 3-11: Abhängigkeit der Selektionsvarianz von der Selektionsintensität
Für dieselbe Selektionsintensität kommt es bei der Truncation-Selektion zu einer deutlich kleineren Selektionsvarianz als bei der linearen Ranking-Selektion bzw. der Turnierselektion, siehe Abbildung 3-11. Dies korrespondiert mit den Ergebnissen aus Abbildung 3-10, in welcher der Loss of diversity verglichen wurde. Ein direkter Vergleich zwischen linearer Ranking-Selektion und Turnierselektion ist nur an den Randpunkten des Definitionsbereiches der linearen Ranking-Selektion möglich. Dort verhalten sich beide Verfahren identisch.
In [BT95] wurde bewiesen, daß sich lineare Ranking-Selektion für einen Selektionsdruck von 2 und Turnierselektion für eine Turniergröße von 2 zueinander identisch verhalten (für beide Verfahren ergeben sich eine identische Selektionsintensität von ![]() ).
).
Für den Einsatz ergibt sich aus dem komplementären Definitionsbereich von linearer Ranking-Selektion und Turnierselektion, daß bei einer Selektionsintensität ![]() lineare Ranking-Selektion zum Einsatz kommt, bei einer Selektionsintensität
lineare Ranking-Selektion zum Einsatz kommt, bei einer Selektionsintensität ![]() Turnierselektion. Mit diesen beiden Verfahren kann damit eine Selektionsintensität und ähnliches Verhalten in einem großen Bereich erreicht werden. Bei Verwendung nur eines der beiden Verfahren wäre dies nicht möglich.
Turnierselektion. Mit diesen beiden Verfahren kann damit eine Selektionsintensität und ähnliches Verhalten in einem großen Bereich erreicht werden. Bei Verwendung nur eines der beiden Verfahren wäre dies nicht möglich.
Welche Aussagen sind bezüglich des Einsatzes von Truncation-Selektion oder der Kombination lineare Ranking-Selektion und Turnierselektion zu machen? Unter der Voraussetzung, daß ein Selektionsverfahren, das bei gleicher Selektionsintensität eine höhere Selektionsvarianz und/oder einen geringeren Loss of diversity aufweist, günstiger ist, wäre die Kombination lineare Ranking-Selektion und Turnierselektion zu bevorzugen. Beide Verfahren haben eine höhere Selektionsvarianz und einen niedrigeren Loss of diversity als die Truncation-Selektion.
Truncation-Selektion hat bei den Problemen Vorteile, bei denen die Suche stärker fokussiert werden soll, ohne einen zu hohen Selektionsdruck ausüben zu müssen. Wie schon weiter oben erwähnt, bekommen bei der Truncation-Selektion die schlechten Individuen gar keine Chance, ausgewählt zu werden. Dies führt, wie in den Abbildungen 3-10 und 3-11 gezeigt, bei gleicher Selektionsintensität zu einem schnelleren Verlust an Information, gleichzeitig aber auch zu einer stärkeren Einengung des Suchbereiches auf vielversprechende Regionen. Wenn zwei Evolutionäre Algorithmen, einer unter Verwendung der Truncation-Selektion, der andere mit der linearen Ranking-Selektion bzw. Turnierselektion, ein und dasselbe Problem mit ansonsten identischen Operatoren und Parametern lösen können, dann ist der Evolutionäre Algorithmus unter Verwendung der Truncation-Selektion schneller.
In mehreren Arbeiten von Mühlenbein und Schlierkamp-Voosen (u.a. [MSV93a], [Müh94]) wurden die Vorteile des Einsatzes der Truncation-Selektion bei der Parameteroptimierung gezeigt. Der von ihnen eingesetzte Breeder Genetic Algorithm verwendet die Truncation-Selektion standardmäßig.
Diese Dokument ist Teil der Dissertation von Hartmut Pohlheim
"Entwicklung und systemtechnische Anwendung Evolutionärer Algorithmen".
This document is part of the .
The is not free.
© Hartmut Pohlheim, All Rights Reserved,
(hartmut@pohlheim.com).