3.4 Mutation |
Durch die Mutation erfolgt eine zufällige Veränderung der Individuen. Diese Veränderungen (Mutationsschritte) sind meist nur relativ gering und werden mit einer geringen Wahrscheinlichkeit (Mutationswahrscheinlichkeit bzw. Mutationsrate) auf die Variablen der Individuen angewendet.
Die Mutation wird im allgemeinen an den Nachkommen durchgeführt, nachdem diese durch Rekombination erzeugt wurden.
Für die Festlegung des angewendeten Mutationsschrittes und der Mutationswahrscheinlichkeit gibt es zwei grundlegend verschiedene Vorgehensweisen: beide Parameter bleiben in ihrer Anwendung während eines Laufs konstant oder es erfolgt eine stetige Anpassung in Abhängigkeit der bereits durchgeführten Mutationen des Laufs. In die erste Kategorie fallen die im folgenden erläuterten Verfahren zur Mutation reeller Variablen, siehe Unterabschnitt 3.4.1, und zur Mutation binärer Variablen, siehe Unterabschnitt 3.4.3. Zur zweiten Kategorie gehören die in Unterabschnitt 3.4.2 erläuterten Verfahren zur Adaption der Schrittweiten der Mutation, die aus dem Bereich der Evolutionsstrategien stammen.
3.4.1 Mutation reeller Variablen |
Mutation bei reellen Variablen bedeutet, daß zufällig erzeugte Werte zu den Variablen mit einer geringen Wahrscheinlichkeit addiert werden. Bei der Mutation reeller Variablen muß damit bestimmt werden, mit welcher Wahrscheinlichkeit eine Variable mutiert wird (Mutationsrate) und wie groß die auszuführenden Veränderungen (Mutationsschritte) sind.
Für die Festlegung der Mutationsrate wurden in verschiedenen Artikeln ähnliche Ergebnisse berichtet. In [MSV93a] wird eine optimale Mutationsrate von 1/n (n: Anzahl der Variablen eines Individuums) angegeben. Dies bedeutet, daß pro Mutation eines Individuums im Durchschnitt genau eine Variable mutiert wird. Ähnliche Ergebnisse wurden in [Bäc93] und [Bäc96] für eine binäre Repräsentation berichtet. Für unimodale Funktionen ist eine Mutationsrate von 1/n die beste Wahl. Eine Erhöhung der Mutationsrate zu Beginn des Laufs verbunden mit einer Verringerung auf 1/n zum Ende des Laufs ergab nur eine minimale Beschleunigung der Suche. Für multimodale Funktionen wurden keine solchen Aussagen gemacht, außer daß eine Adaption der Mutationsrate sinnvoll sein müßte. Die hier angegebenen Werte für die Mutationsrate gelten für separierbare Funktionen. Die meisten in praktischen Anwendungen anzutreffenden Funktionen sind allerdings nicht vollständig separierbar. Für diese Funktionen sind aber keine anderen Angaben verfügbar, so daß auch hier die Verwendung einer Mutationsrate von 1/n empfohlen wird.
Die Bestimmung der Größe des Mutationsschrittes ist schwierig. Einerseits hängt die beste Schrittweite von der Art des Problems ab, und andererseits kann sich die beste Schrittweite während eines Laufs verändern. Es ist allerdings bekannt, daß vorteilhafte Mutationen meist kleine Veränderungen der Variablen als Grundlage haben. Dies trifft besonders für den Fall zu, wenn ein Individuum schon gut angepaßt ist. Anders ist die Situation, wenn neue Bereiche erkundet werden. In diesem Fall können größere Veränderungen schnell zu einem Erfolg führen. Als Schlußfolgerung kann abgeleitet werden, daß ein Mutationsoperator oft mit kleinen Mutationsschritten arbeiten sollte, aber ab und zu auch große Mutationsschritte angewendet werden.
In [MSV93a] und [Müh94] wurde solch ein Operator vorgestellt (Mutationsoperator des Breeder Genetic Algorithm - BMc und BMd):
Dieser Algorithmus ist in der Lage, die meisten Punkte in einem Hyperwürfel zu generieren, der durch die Variablen des Individuums und den möglichen Bereich der Mutation (definiert durch den Parameter r (range) und den Definitionsbereich der Variablen) aufgespannt wird. Es werden mit einer hohen Wahrscheinlichkeit Individuen erzeugt, die sehr nah an dem nicht mutierten Individuum liegen und nur wenige Individuen, die weiter weg vom Ausgangsindividuum liegen. Abbildung 3-18 versucht davon einen Eindruck zu vermitteln.
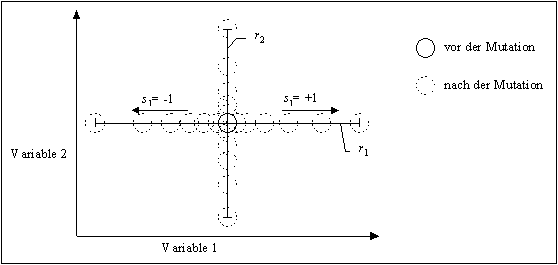
Abbildung 3-18: Mögliche Positionen eines Individuums nach der Mutation reeller Parameter
Der Präzisionsparameter k bestimmt die minimal zu erzeugende Mutationsschrittweite. Für beide Varianten, kontinuierlich und diskret, beträgt die minimale Schrittweite 2-k. Bis zu dieser Genauigkeit kann das Optimum einer Funktion erreicht werden. Der größte Schritt beträgt 1. Daraus ergibt sich ein Bereich für die Mutationsschritte von [r, r·2-k].
Der in Gleichung 3-19 angegebene Mutationsoperator mutiert mit einer Mutationsrate von 1/n, d.h., es wird nur eine Variable pro mutiertem Individuum verändert. Wie schon weiter oben angedeutet, können dadurch nur separierbare Funktionen sicher bearbeitet werden. Bei nicht separierbaren Funktionen kommt es mit einer hohen Wahrscheinlichkeit zu einem Steckenbleiben der Optimierung, da ab einer bestimmten Anpassung des Individuums durch Veränderung nur einer Variablen keine Verbesserung erreicht werden kann.
In [SVM96] wurde eine Erweiterung des Mutationsoperators aus Gleichung 3-19 vorgestellt, die dieses Problem ansatzweise mindert. Durch die Erweiterung wird jetzt nicht genau eine Variable mutiert, sondern zusätzlich werden auch die anderen Variablen des Individuums mutiert; allerdings sind bei diesen die Veränderungen wesentlich geringer. Dazu wurde ein dritter Parameter v eingeführt, der die Verteilung des bisher auf eine Variable beschränkten Mutationsschrittes auf die anderen Variablen dieses Individuums steuert.
Verteilte Mutation reeller Variablen (BMv):
Diese verteilte Mutation reeller Variablen führt dazu, daß eine Variable mit Index i wie bisher mutiert wird. Zusätzlich werden alle anderen Variablen auch mutiert, wobei die Größe des Mutationsschrittes mit steigendem Abstand zur Variablen i exponentiell abnimmt. Dies führt zu einer verkoppelten Veränderung der Variablen, die zueinander benachbart sind. Damit ist dieser Mutationsoperator besser für die Bearbeitung von Funktionen geeignet, bei denen benachbarte Variablen miteinander verkoppelt sind. Für einen Wert des Verteilungsparameters v von v = 0 ergibt sich der Mutationsoperator aus Gleichung 3-19.
Typische Werte für die Parameter der Mutationsoperatoren aus Gleichung 3-19 und 3-20 sind:
 (3-21)
(3-21)
Durch eine Veränderung dieser Parameter können sehr unterschiedliche Suchstrategien des Mutationsoperators eingestellt werden:
Für eine Veränderung der Parameter der Mutationsoperatoren während eines Laufs gibt es zwei Möglichkeiten:
Die in diesem Unterabschnitt in Gleichung 3-19 und 3-20 vorgestellten Mutationsoperatoren für reelle Variablen führen mit den hier angegebenen Parametereinstellungen für eine große Klasse von praktisch auftretenden Zielfunktionen eine robuste Suche durch.
3.4.2 Mutation reeller Variablen mit Adaption der Schrittweiten |
Für die Durchführung der Mutation reeller Variablen gibt es die Möglichkeit, Richtung und Schrittweite erfolgreicher Mutationen durch Adaption dieser Größen zu erlernen. Solche Mutationsverfahren sind z.B. Bestandteil der Evolutionsstrategien [Sch81] und der Evolutionären Programmierung [Fdb95]. Weiterentwicklungen dieser Verfahren bzw. neue Verfahren wurden in den letzten Jahren in mehreren Arbeiten veröffentlicht:
Um die zu adaptierenden Schrittweiten und Richtungen zu speichern, werden an jedes Individuum zusätzliche Variablen angehängt. Die Anzahl dieser zusätzlichen Variablen ist abhängig von der Anzahl der Variablen n und dem Verfahren. Für die Speicherung der adaptierten Schrittweiten werden n zusätzliche Schrittweiten und für die Speicherung einer adaptierten Richtung n zusätzliche Variablen benötigt. Für die Speicherung von n Richtungen würden damit n2 zusätzliche Variablen benötigt.
Weiterhin ist zu beachten, daß für die Adaption von n Schrittweiten n Generationen mit jeweils mehreren Individuen berechnet werden müssen. Bei n Schrittweiten und einer Richtung (A II) erhöht sich diese Zahl auf 2n Generationen und bei n Richtungen auf n2 Generationen.
Aus dem Speicherbedarf für zusätzliche Parameter und den notwendigen Berechnungen zur Adaption der Schrittweiten und Richtungen ergibt sich, daß nur die ersten beiden Verfahren für die praktische Anwendung relevant sind. Nur diese beiden führen die Adaption mit einem vertretbaren Aufwand durch. Die Adaption von n Richtungen (A I) läßt sich mit den heute zur Verfügung stehenden Mitteln nur auf kleine Probleme anwenden.
Die Algorithmen für die Mutationsoperatoren mit Schrittweitenanpassung sollen hier nicht wiedergegeben werden, da diese komplex und lang sind. Statt dessen wird auf die oben genannten Arbeiten verwiesen, in denen die Algorithmen beschrieben sind. Eine Beispielimplementierung ist außerdem in [Poh96] gegeben. Auf weitere Anmerkungen, die für die Anwendung wichtig sind und nicht bzw. nur teilweise in den obigen Arbeiten enthalten sind, wird im folgenden eingegangen.
Die Mutationsoperatoren mit Schrittweitenanpassung benötigen eine etwas andere Parametrisierung des Evolutionären Algorithmus, als die anderen Mutationsoperatoren für reelle Variablen. Sie arbeiten mit einer geringen Anzahl von Individuen, die jeweils viele Nachkommen produzieren. Von den Nachkommen werden nur die besten in die Population eingefügt, wobei alle Eltern ersetzt werden. Der Selektionsdruck ist 1, da alle Individuen gleich viele Nachkommen produzieren. Eine Rekombination wird nicht durchgeführt. Übliche Werte und Bereiche dieser Parameter sind:
Beim Einsatz dieser Mutationsoperatoren zeigte sich ein Problem sehr deutlich: die Festlegung der Anfangsgröße der individuellen Schrittweiten. In den Veröffentlichungen ist dort nur ein Wert von eins für alle Schrittweiten angegeben. Mit diesem Wert können aber nur einige Testfunktionen gut gelöst werden, bei denen zusätzlich alle Variablen denselben Definitionsbereich besitzen. Für die praktische Anwendung müssen die individuellen Anfangsschrittweiten in Abhängigkeit des Definitionsbereiches der Variablen festgelegt werden und zusätzlich sollte eine problemabhängige Skalierung der Größenordnung der Anfangsschrittweiten stattfinden. Dafür bietet sich, analog zu den im vorigen Unterabschnitt erläuterten Mutationsoperatoren für reelle Variablen, die Verwendung des Parameters Mutationsbereich r an.
Typische Werte für den Mutationsbereich zur Festlegung der Anfangsschrittweiten sind:
![]() (3-22)
(3-22)
Dieser Mutationsbereich bestimmt nur die Initialisierung der Schrittweiten zu Beginn eines Laufs. Bei der nachfolgenden Schrittweitenanpassung sind die Schrittweiten nicht beschränkt.
Ein größerer Wert für den Mutationsbereich hat zur Folge, daß die individuellen Schrittweiten zu Beginn groß sind. Dadurch werden die Nachkommen weiter entfernt von den Eltern erzeugt. Dies führt am Anfang zu einer groben Suche. Ein kleiner Wert für den Mutationsbereich dagegen bedingt eine anfänglich feinere Suche. In der praktischen Anwendung muß zwischen diesen beiden Extremen abgewogen werden. Bei einer zu groben Suche kann es passieren, daß keine Adaption der Schrittweiten stattfindet, die Suche kommt nicht vorwärts. Eine zu feine Suche andererseits kann erstens sehr lange benötigen, bis es zu einer gerichteten Suche kommt und zweitens in jedem kleinen lokalen Minimum steckenbleiben.
Der Einsatz der in diesem Unterabschnitt besprochenen Mutationsoperatoren ist besonders bei solchen Problemen vielversprechend, die korrelierte Variablen enthalten. Durch die Adaption der Schrittweiten können die Wechselbeziehungen zwischen den Variablen erlernt werden. Manche Probleme, wie z.B. Rosenbrock's Funktion (enthält ein schmales und gebogenes Tal), können dadurch sehr schnell und gut gelöst werden.
Schwierig wird der Einsatz dieser Mutationsoperatoren, wenn die Zielfunktion verrauscht ist bzw. viele kleine Minima aufweist. Dann bleiben diese Operatoren in einem der lokalen Minima hängen.
3.4.3 Mutation binärer Variablen |
Die Mutation von Individuen mit binären Variablen bedeutet das Umschalten der Variablenwerte, da jede Variable nur zwei Zustände haben kann. Die Länge des Mutationsschrittes ist damit immer 1. Für jedes Individuum werden die zu verändernden Variablen ausgewählt (meist gleichverteilt zufällig) und dann die Mutation durchgeführt. Tabelle 3-1 veranschaulicht diesen Vorgang für ein Individuum mit 1 Variablen, von denen Variable 4 mutiert wird.
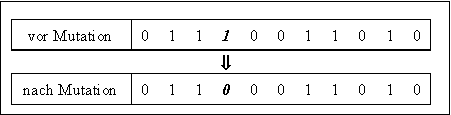
Tabelle 3-1: Mutation eines Individuums mit binären Variablen
Bisher wurde davon ausgegangen, daß die Repräsentation eines Individuums identisch zur Repräsentation des zu lösenden Problems ist. Dies ist aber nicht immer so. Gerade im Bereich der Genetischen Algorithmen werden Probleme, deren Variablen reelle oder ganzzahlige Zahlen sind, in eine binäre Repräsentation umgewandelt und auf diese binäre Repräsentation wird ein Evolutionärer Algorithmus angewendet. Für die Umwandlung der binären Repräsentation in reelle Zahlen können verschiedenen Kodierungen und Skalierungen verwendet werden. Die am meisten verwendeten Kodierungen sind die binäre und die gray Kodierung. Zusätzlich kann statt einer linearen Skalierung eine logarithmische Skalierung verwendet werden. Die Auswirkungen der verschiedenen Kodierungen und Skalierungen auf ein und dasselbe Individuum mit binären Variablen zeigt Tabelle 3-2. Dabei wird angenommen, daß das Individuum in Tabelle 3-1 eine reelle Zahl im Bereich [1, 10] kodiert.
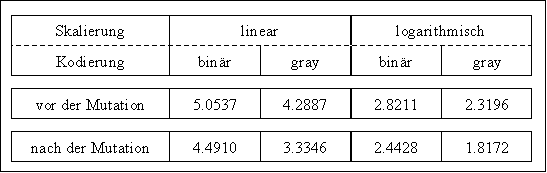
Tabelle 3-2: Ergebnis und Auswirkungen einer binären Mutation für unterschiedliche Skalierungen und Kodierungen, wenn das Individuum in Tabelle 3-1 eine reelle Zahl im Bereich [1, 10] repräsentiert
Welche Kodierung die günstigere ist, hängt stark vom zu lösenden Problem ab. Dafür lassen sich keine einheitlichen Aussagen machen. Einige Arbeiten berichteten bessere Ergebnisse bei Verwendung der gray Kodierung (u.a. [CS88]). Jones und Forrest [JF95] untersuchten die Schwere einer Anzahl bekannter Testfunktionen für einen Genetischen Algorithmus. Dabei wurde auch die Abhängigkeit von binärer und gray Kodierung untersucht. In ihren Untersuchungen war es von der Länge der Kodierung abhängig, welche Kodierung etwas günstiger war. Als Maß verwendeten sie die Fitneß-Distanz-Korrelation, siehe Abschnitt 5.4.2, S.. Aus den Ergebnissen ihrer Untersuchung läßt sich schlußfolgern, daß es keine allgemeine Empfehlung für eine Kodierung geben kann.
Die Anwendung der linearen oder logarithmischen Skalierung ist problemabhängig, kann aber vom Anwender besser überblickt werden als die Auswahl der zu verwendenden Kodierung. Bei der logarithmischen Skalierung wird die Variable nicht über den gesamten Wertebereich gleichmäßig diskretisiert, sondern im unteren Teil des Definitionsbereiches der Variablen findet eine feinere Diskretisierung als im oberen Teil statt. Dies kann zum einen die Suche im wenig erfolgversprechenden oberen Teil verkürzen und gleichzeitig die erreichbare Genauigkeit im fein diskretisierten unteren Teil erhöhen.
Mit den zur Verfügung stehenden leistungsfähigen Mutationsoperatoren für reelle Variablen besteht allerdings kein Grund für die Kodierung reeller Variablen in eine binäre Repräsentation und die Anwendung entsprechender Operatoren. Die Vorteile des Einsatzes von Operatoren für reelle Variablen wurden in verschiedenen Arbeiten gezeigt (u.a. [Mic94] und [Dav91]).
Diese Dokument ist Teil der Dissertation von Hartmut Pohlheim
"Entwicklung und systemtechnische Anwendung Evolutionärer Algorithmen".
This document is part of the .
The is not free.
© Hartmut Pohlheim, All Rights Reserved,
(hartmut@pohlheim.com).