4.4.1 Topologie von Nachbarschaften
4.4.2 Allgemeine Beschreibung von Nachbarschaften
4.4.3 Selektion in Nachbarschaft
4.4 Lokales Modell |
Beim lokalen Modell (auch Diffusionsmodell oder Nachbarschaftsmodell genannt) wird jedes Individuum als ein separates Element betrachtet. Eine Interaktion findet nur mit den Individuen in der näheren Umgebung statt (und nicht mit denen der Unterpopulation oder der gesamten Population). Die Reichweite der Selektion ist beim lokalen Modell auf die festgelegte Nachbarschaft eines Individuums beschränkt, die Nachbarschaft entspricht dem Selektionspool. Dadurch findet eine fließende Unterteilung der Gesamtpopulation statt. Die Individuen sind untereinander durch die Distanz zwischen ihnen isoliert, je größer die Distanz, um so größer ist die Isolation. Dieser Effekt wird als Isolation durch Distanz bezeichnet.
Das lokale Modell wird durch eine Anzahl von Parametern bestimmt:
Die Topologie der Nachbarschaft und die Distanz zu den Nachbarn bestimmen die Art und Größe einer Nachbarschaft. Durch die Wahl dieser Parameter kann beeinflußt werden, wie schnell sich Informationen innerhalb der Population ausbreiten können. Damit wird beeinflußt, ob sich die Population eher wie lose miteinander gekoppelte Bereiche oder wie stark verbundene Bereiche (ähnlich einer Gesamtpopulation mit dem globalen Modell) entwickelt.
Die Selektion innerhalb der Nachbarschaft und das Wiedereinfügen der Nachkommen in die Nachbarschaft verläuft ähnlich wie bei den entsprechenden Verfahren für eine Population. Auf Grund der oft sehr kleinen Größe der Nachbarschaften können jedoch zusätzlich Spezialfälle betrachtet werden.
4.4.1 Topologie von Nachbarschaften |
Bei der Erläuterung der Topologien, in denen Migration beim regionalen Modell stattfindet (Unterabschnitt 4.3.2, ab S.), wurden einige Varianten für Nachbarschaftstopologien aufgezeigt. Die dort gemachten Angaben gelten übertragen auch für das lokale Modell.
Während beim regionalen Modell jeder Knoten eine Unterpopulation repräsentiert, besteht beim lokalen Modell jeder Knoten aus einem Individuum. Die Zahl der Individuen ist beim lokalen Modell im allgemeinen deutlich größer als die Anzahl der Unterpopulationen beim regionalen Modell. Daher haben sich andere Topologien im Einsatz durchgesetzt bzw. die Beschreibung ist etwas anders.
In diesem Unterabschnitt wird eine Auswahl der gebräuchlichsten Topologien für lokale Modelle vorgestellt. Im Unterabschnitt 4.4.2, S., wird eine allgemeine Beschreibung für Nachbarschaftstopologien gegeben, in der alle bis dahin aufgeführten Topologien des regionalen und lokalen Modells als Spezialfälle eingeordnet werden können.
Die gebräuchlichsten Topologien von Nachbarschaften können in die folgenden Bereiche unterteilt werden:
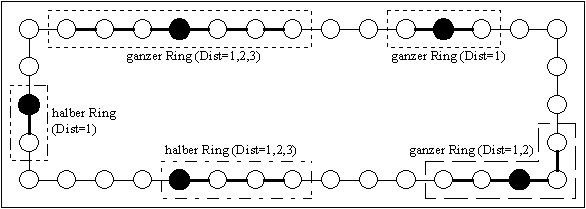
Abbildung 4-8: Lineare Nachbarschaftstopologien: ganzer und halber Ring mit unterschiedlicher Distanz
Durch die Distanz Dist zu den Nachbarn wird zusammen mit der Topologie die Größe der Nachbarschaft festgelegt. Die Größe der Nachbarschaft bestimmt einmal den Selektionsdruck, der bei der Auswahl von Individuen in dieser Nachbarschaft herrscht. Außerdem wird durch die Größe der Nachbarschaft die Geschwindigkeit der Ausbreitung von Informationen innerhalb der Population gesteuert. Bei großen Nachbarschaften kommt es zu einer schnellen Ausbreitung von Information, bei kleinen Nachbarschaften zu einer langsamen.
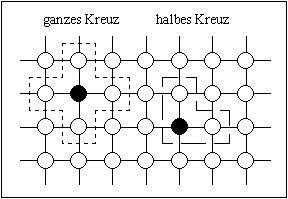
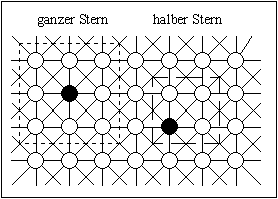
Abbildung 4-9: Zweidimensionale Nachbarschaftstopologien; links: ganzes und halbes Kreuz, rechts: ganzer und halber Stern, alle mit einer Distanz von 1
Eine hohe Ausbreitungsgeschwindigkeit hat zur Folge, daß sich das Verhalten des lokalen Modells dem des globalen Modells annähert. Bei einer langsamen Informationsausbreitung kommt es zu einer fließenden Isolation räumlich entfernter Bereiche der Population, zu einer 'Isolation durch Distanz'.
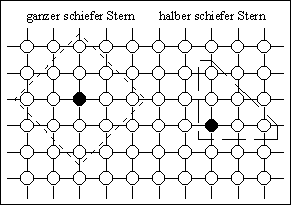
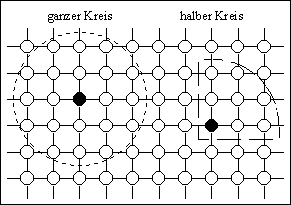
Abbildung 4-10: Zweidimensionale Nachbarschaftstopologien; links: ganzer und halber schiefer Stern mit einer max. Distanz von 2, rechts: ganzer und halber Kreis mit einer max. Distanz von ![]()
4.4.2 Allgemeine Beschreibung von Nachbarschaften |
Bei der Beschreibung der Migrationstopologien des regionalen Modells in Unterabschnitt 4.3.2, S. und der Nachbarschaftstopologien des lokalen Modells in Unterabschnitt 4.4.1, S. wurden für die einzelnen Topologien und Nachbarschaften verschiedene Namen verwendet. Diese Namen haben sich in der bisherigen Anwendung durchgesetzt. Sie haben aber den Nachteil, daß ein direkter Vergleich der verschiedenen Topologien schwierig und eine Erweiterung auf beliebige Dimensionen nicht offensichtlich ist. In diesem Unterabschnitt wird eine allgemeine Definition von Nachbarschaften gegeben, die sich auf beliebige Dimensionen ausdehnen läßt und alle bisherigen Topologien als Spezialfälle enthält.
Die Beschreibung wird auf Knoten (Unterpopulationen beim regionalen Modell bzw. Individuen beim lokalen Modell) und Kanten (Verbindungen zwischen Knoten) bezogen. Ziel dieser Beschreibung ist es, die Indizes der Knoten zu errechnen, die zu einem gegebenen Knoten und einer gewünschten Nachbarschaftstopologie die Nachbarn dieses Knotens sind.
Für die Beschreibung der Nachbarschaften werden die folgenden Dinge vorausgesetzt:
Für eine allgemeine Beschreibung ist es notwendig, daß die Knoten in beliebig vielen Dimensionen angeordnet werden können und die Ausdehnung jeder Dimension beliebig festgelegt werden kann. Im folgenden wird die Anzahl der Dimensionen der Anordnung durch Dim angegeben werden und die Anzahl der Knoten in jeder Dimension ist im Vektor LenDim (length of dimension) enthalten. (Jede niedrigere Dimension läßt sich aus einer höheren Dimension ableiten, indem die Anzahl der Knoten aller höheren Dimensionen auf 1 gesetzt wird.)
Die Anzahl der Knoten einer Anordnung AnzKnoten läßt sich aus der Anzahl der Knoten pro Dimension berechnen:
![]() (4-5)
(4-5)
Der Index eines Knoten in der eindimensionalen Indexierung, IxKnoten, läßt sich aus seiner mehrdimensionalen Indexierung, IxDimKnoten, ermitteln. IxDimKnoten ist ein Vektor der Länge Dim.
Ausgehend von einem Knoten kann der Index jedes anderen Knotens in der Anordnung relativ angegeben werden. Dies kann mehrdimensional, IxRelDimKnoten, oder eindimensional, IxRelKnoten, erfolgen. Eine Umrechnung zwischen beiden Angaben ist mit Gleichung 4-6 möglich. Bei der mehrdimensionalen Angabe enthält jedes Element von IxRelDimKnoten den rechtwinkligen Abstand in der jeweiligen Dimension. Eine Angabe von IxRelDimKnoten=[3,4,2] bedeutet, daß die Knoten in Dimension 1 einen Abstand von 3, in Dimension 2 einen Abstand von 4 und in Dimension 3 einen Abstand von 2 haben. Wenn der Abstand von einem Knoten zum anderen gerichtet betrachtet wird, nehmen die Angaben auch negative Werte an.
Der direkte Abstand zwischen zwei Knoten läßt sich einmal aus der absoluten Position beider Knoten oder aus der relativen Position der Knoten zueinander berechnen:
 (4-7)
(4-7)
Für jeden Knoten lassen sich bestimmen:
Auf der Grundlage dieser Variablen und Begriffe lassen sich jetzt verschiedenste Nachbarschaften definieren, die über alle Dimensionen skaliert werden können. Für die eindeutige Auswahl einer Nachbarschaft reichen dann die folgenden drei Parameter aus:
Die folgenden Definitionen entsprechen den vollen Nachbarschaften. Aus einer vollen Nachbarschaft läßt sich die halbe Nachbarschaft ableiten, indem alle Knoten aus der Nachbarschaft entfernt werden, in denen mindestens einer der relativen Indizes (Element von IxRelDimKnoten) negativ ist.
Für die Benennung werden meistens die Namen der Topologien verwendet, die für die zweidimensionale Topologie gebräuchlich sind. Der Vorsatz Hyper- drückt aus, daß dieser Begriff über alle Dimensionen gültig sein soll. Außerdem wird angegeben, welcher gebräuchlichen Topologie dies in einer und zwei Dimensionen entspricht.
1. Hyperkreuz:
![]()
2. Hyperstern:
;
3. schiefer Hyperstern:
;
4. Hyperkugel:
Mit diesen allgemein definierten Nachbarschaftstopologien lassen sich die bekannten und gebräuchlichen Nachbarschaftstopologien angeben und können dadurch als Grundlage weiterer Untersuchungen dienen.
Für einen Vergleich der verschiedenen Nachbarschaften müssen einige Maßzahlen definiert werden, die bestimmte Eigenschaften einer jeden Nachbarschaft wiedergeben. Dabei ist N die Anzahl der Knoten einer Nachbarschaft.
Radius einer Nachbarschaft:
Durch Verwendung aller Knoten einer Anordnung in Gleichung 4-8 läßt sich der Radius einer Anordnung RadiusAnord berechnen. Der Quotient aus RadiusNach und RadiusAnord (Radienquotient) ist eine Maßzahl, die zum Vergleich einiger Anordnungen und Nachbarschaften untereinander verwendet werden kann.
Die hier vorgestellte allgemeine Beschreibung der Nachbarschaftstopologien und ihre einfache Definition in Abhängigkeit weniger Parameter sollte als Grundlage für weitere Arbeiten dienen.
4.4.3 Selektion in Nachbarschaft |
Die Auswahl der Individuen zur Bildung der Nachkommen erfolgt beim lokalen Modell in zwei Schritten. Zuerst wird über die Population verteilt eine Anzahl von Individuen als Zentrum einer Nachbarschaft festgelegt. Um diese Individuen wird dann jeweils die Nachbarschaft definiert. Im zweiten Schritt werden aus den Nachbarschaften die Individuen zur Produktion der Nachkommen ausgewählt.
Jeder dieser Selektionsschritte kann mit unterschiedlichen Methoden realisiert werden:
1. Auswahl der Zentren der Nachbarschaften:
2. Auswahl innerhalb einer Nachbarschaft:
In der Anwendung sind zwei Bereiche zu unterscheiden: Verwendung einer parallelen und einer seriellen Implementierung.
Bei einer parallelen Implementierung, bei der jedes Individuum einem Prozessor zugeordnet ist, wird in jeder Generation ein neues Individuum pro Prozessor berechnet. Deshalb bietet es sich an, daß jedes Individuum Zentrum einer Nachbarschaft ist und sich einen zweiten Elter in der Nachbarschaft nach einem einfachen und schnellen Verfahren sucht, z.B. bester oder zufälliger Nachbar.
Bei einer seriellen Implementierung dagegen kann die Anzahl der Nachkommen pro Generation kleiner als die Anzahl der Individuen in der Population sein (definiert durch den Parameter generation gap). Für die Auswahl der Eltern ergeben sich dadurch die oben vorgestellten Möglichkeiten, die eine erweiterte Kontrolle des Selektionsdruckes zulassen.
4.4.4 Wiedereinfügen in Nachbarschaft |
Nachdem die Nachkommen gebildet und bewertet wurden, müssen diese wieder in die Population eingefügt werden. Durch die Verwendung einer lokalen Nachbarschaft, in der alle Prozesse stattfinden, müssen die Nachkommen einer Nachbarschaft in genau diese Nachbarschaft eingefügt werden. Dieser Prozeß wird als lokales Wiedereinfügen bezeichnet (im Gegensatz zum globalen/regionalen Wiedereinfügen aus Abschnitt 3.5, ab S.).
Das Wiedereinfügen der Nachkommen in die Nachbarschaft kann nach zwei Kriterien gegliedert werden: Welche Nachkommen werden in die Nachbarschaft eingefügt? Welche Individuen der Nachbarschaft werden dadurch ersetzt?
Das Verfahren zur Auswahl der Nachkommen bestimmt den Selektionsdruck, der auf die Nachkommen wirkt, bevor diese in die Population eingefügt werden. Das Einfügen aller Nachkommen hat keinen Selektionsdruck zur Folge. Wenn nur Nachkommen eingefügt werden, die besser als die schlechtesten Individuen sind, so kommt es zu einer kontinuierlichen Verbesserung der durchschnittlichen Güte der Population. Wenn die Nachkommen besser als die Eltern sein müssen, dann entspricht dies dem höchsten Selektionsdruck, da die Eltern nicht die schlechtesten Individuen der Nachbarschaft sind. Durch diesen hohen Selektionsdruck kann es aber zu einem Steckenbleiben der Entwicklung der Population kommen, denn in den meisten Fällen ist nur ein kleiner Teil der Nachkommen besser als die Eltern.
Das Ersetzen der Individuen in der Nachbarschaft bestimmt, ob eine elitest Methode angewendet wird oder nicht. Beim gleichmäßigen Ersetzen der Individuen in der Nachbarschaft können die besten Individuen durch schlechtere Nachkommen ersetzt werden. Dasselbe gilt, wenn die Eltern ersetzt werden und die Nachkommen nicht besser als die Eltern sein müssen. Nur wenn die schlechtesten Individuen der Nachbarschaft ersetzt werden, ist gewährleistet, daß die besten Individuen in der Population überleben bzw. nur durch bessere Nachkommen ersetzt werden.
Für die Anwendung wird deshalb empfohlen, in der Nachbarschaft die schlechtesten Individuen durch die Nachkommen zu ersetzen. Als Nachkommen können die ausgewählt werden, die besser als die schlechtesten Individuen sind (empfohlene Methode) oder alle Nachkommen können verwendet werden.
4.4.5 Analyse des lokalen Modells |
Durch die auf Nachbarschaften beschränkte Selektion findet eine lokale Interaktion zwischen den Individuen statt, es ergibt sich eine `Isolation durch Distanz'. In Abhängigkeit der Nachbarschaften kann die Auswirkung der lokalen Interaktion (der Austausch von Informationen) auf die gesamte Population beeinflußt werden. Je größer die Ausdehnung der Nachbarschaft, um so größer sind die Überlappungen zwischen den einzelnen Nachbarschaften und um so schneller werden Informationen in der gesamten Population ausgetauscht. Durch die Größe der Nachbarschaft kann somit zwischen einer schnellen Ausbreitung von Informationen oder der Erhaltung der Verschiedenartigkeit der einzelnen Bereiche der Population (langsame Ausbreitung) gewählt werden.
Meist wird eine hohe Verschiedenartigkeit innerhalb der Population angestrebt, da hiermit Probleme, wie die vorzeitige Konvergenz (premature convergence) in ein lokales Minimum, verhindert werden können. Das lokale Modell mit einer kleinen Nachbarschaft arbeitet oft besser als das lokale Modell mit einer großen Nachbarschaft. Trotzdem ist es wichtig, daß die Verbindungen innerhalb der Population erhalten bleiben. Ähnliche Ergebnisse wurden aus Berechnungen in [VSB92] abgeleitet (Verwendung einer kleinen zweidimensionalen Struktur, halber Stern, mit einer Distanz von 1; bei größeren Populationen (>100 Individuen) sollte eine entsprechend größere zweidimensionale Nachbarschaft bzw. eine größere Distanz verwendet werden).
Im Verlauf der Anwendung des lokalen Modells bilden sich über die Generationen virtuelle Inseln in der Population (Visualisierung der Zielfunktionswerte der Individuen in ihrer Nachbarschaft). Die virtuellen Inseln verändern ständig ihre Größe und Position. Einen Eindruck davon vermittelt Abbildung 5-11, S., die sich im Verlauf der Generationen verändernde virtuelle Inseln zeigt.
Der erfolgreiche Einsatz des lokalen Modells wurde seit Ende der 80er Jahre oft berichtet. Der von der Gruppe um Mühlenbein ([MGK88], [Müh89], [MSB91]) entwickelte Parallel Genetic Algorithm (PGA) verwendete lokale Selektion in einer zweidimensionalen Struktur (ganzer Stern mit einer Distanz von 1, dadurch 4 Nachbarn). Durch die Verteilung der Individuen und die starke Lokalität wurde eine fast 100%ige Auslastung der Prozessoren und eine annähernd lineare Beschleunigung der Berechnungen erreicht. Da sich der PGA leicht auf viele Prozessoren verteilen ließ, konnten sehr große Probleme gelöst werden.
Eine spezielle Struktur der Nachbarschaft wurde von Gorges-Schleuter in [GS91] vorgestellt, genannt ASPARAGOUS. Die Individuen wurden auf den Eckpunkten einer ringförmigen Leiter angeordnet (ähnlich der Leiterstruktur in Abbildung 4-6, S.). Neben der guten Performanz wurde eine superlineare Beschleunigung gegenüber einer einzigen Population gleicher Individuenzahl erreicht. Unter anderem wurden neue Optima für sehr große Probleme gefunden.
Manderick und Spiessens ([MS89], [SM91]) berichten von der Implementierung des lokalen Modells eines Genetischen Algorithmus auf einem massiv parallelen Rechner. Dabei untersuchten sie den Einfluß der gewählten Selektionsmethode.
Collins und Jefferson [CJ91] untersuchten verschiedene Selektionsmethoden und verglichen das lokale Modell mit einer einheitlichen Gesamtpopulation. Das lokale Modell war deutlich schneller und robuster als eine Gesamtpopulation. Besonders bei der Lösung schwieriger Probleme war die Lokalität des lokalen Modells von Vorteil, da sich verschiedene Nischen mit Lösungen etablieren konnten, was zu einer robusteren Suche führte.
Davidor [Dav91a] verwendete ein zweidimensionales lokales Modell (mit ganzem Stern und Distanz 1, dadurch 8 Nachbarn) und beschrieb die Herausbildung lokaler Nischen und Inseln mit homogeneren Individuen und Fitneßwerten, die jeweils nahe der lokalen Optimalität lagen. Im Verlauf der Optimierung näherten sich diese Inseln dem lokalen Optimum an und einige Inseln mit besonders guten Individuen breiteten sich über große Teile der Population aus, wodurch Inseln mit Individuen schlechter Fitneß ausstarben. Davidor verwies darauf, daß sich seine Beschreibung auf größere Dimensionen verallgemeinern läßt.
Gordon und Whitley [GW91] verglichen verschiedene parallele Implementierungen an einer Reihe von Testfunktionen, wobei das lokale Modell (cellular GA) über alle Testfunktionen eine etwas schlechtere Performanz als die Migrationsmodelle hatte, bei einigen der Testfunktionen war es dagegen wesentlich besser.
Von Schwehm wurde in [Swm96] eine Analyse verschiedener paralleler Implementierungen einschließlich des lokalen Modells vorgenommen. Er untersuchte u.a. den Einfluß der Größe der Nachbarschaft und der Nachbarschaftsstruktur des lokalen Modells auf das Konvergenzverhalten ([Swm96], S.116-124). Für kleine Nachbarschaftsgrößen wurden weniger Zielfunktionsaufrufe benötigt, als für große Nachbarschaftsgrößen. Allerdings durfte die Nachbarschaft auch nicht zu klein sein. Bei genauerer Untersuchung zeigte sich, daß bei einer zu großen Nachbarschaft die Diversität in der Population sehr schnell stark abnahm, was zu einer Verlangsamung der Suche führte. Bei einem Vergleich verschiedener Nachbarschaftsstrukturen konnten keine eindeutigen Unterschiede zwischen den verschiedenen Nachbarschaften festgestellt werden. Dies zeigte sich noch deutlicher, als für jede Nachbarschaft einige der weiteren Parameter optimal eingestellt wurden. Jetzt waren die vorher noch erkennbaren Unterschiede fast vollständig verschwunden. Nur zwei Strukturen (binärer Baum und Ring) waren schlechter als die anderen: beide hatten einen sehr großen Durchmesser der Anordnung sowie eine kleine Anzahl von Nachbarn, die jeweils einen geringen Abstand zueinander hatten. Bei anderen Strukturen (shuffle-exchange) mit vergleichbarem Durchmesser und vergleichbarer Anzahl von Nachbarn, die aber ein besseres Konvergenzverhalten zeigten, waren die Nachbarn dagegen weiter voneinander entfernt. Daraus kann wiederum die Schlußfolgerung gezogen werden, daß die Bereiche der Population nicht zu stark voneinander isoliert sein dürfen. Die Verbindung zwischen allen Bereichen der Population muß gewährleistet sein.
Von Sarma und DeJong wurde in [SDJ96] eine Untersuchung des Einflusses der Nachbarschaftsstruktur und -größe auf die Selektionsintensität innerhalb der Population vorgenommen. Die Untersuchung war auf zweidimensionale quadratische Anordnungen unterschiedlicher Größe beschränkt. Die untersuchten Nachbarschaftsstrukturen waren alle volle Strukturen (Kreuz mit maximalen Abstand von 1 (als L5 bezeichnet) und 2 (L9), Stern mit maximalem Abstand von 1 (C9) und schiefer Stern mit maximalem Abstand von 2 (C13)). Sarma und DeJong kamen zu der Schlußfolgerung, daß der Quotient (Radienquotient) aus dem Radius der Nachbarschaft RadiusNach und dem Radius der Anordnung RadiusAnord zur Charakterisierung der Selektionsintensität in der Population ausreichend ist.
Diese Aussage läßt sich für die von Sarma und DeJong verwendeten Anordnungen und Nachbarschaftsstrukturen verwenden, die Spezialfälle und Vereinfachungen darstellen. Außerdem kann sie zum Vergleich von Anordnungen und Strukturen verwendet werden, die jeweils nur in ihrer Ausdehnung verändert werden, wobei die relative Größe zueinander erhalten bleibt. Aber schon beim Vergleich von vollen Nachbarschaftsstrukturen mit halben Nachbarschaftsstrukturen ist der einfache Parameter Quotient aus dem Radius der Nachbarschaft und dem Radius der Anordnung nicht mehr ausreichend. Weitere Größen müssen einbezogen werden, wenn die Anordnung nicht quadratisch ist. In dieser Richtung ist noch Arbeit zu leisten.
Die Selektionsintensität in der Population ist unter Verwendung derselben Selektionsintensität in den jeweiligen Selektionspools bei einer lokalen Selektion und kleinen Radienquotienten kleiner, als bei einer globalen Selektion. Dies ist im Prinzip der lokalen Selektion begründet. Mit steigendem Radienquotient nähert sich die Selektionsintensität der lokalen Selektion dem der globalen Selektion an (Sarma und DeJong stellten fest, daß bei einem Radienquotient von 0.5 die lokale Selektion die Selektionsintensität der globalen Selektion erreicht.). Ziel der Anwendung des lokalen Modells kann es nicht sein, dieselbe Selektionsintensität wie bei einer globalen Population mit gleich vielen Individuen zu erreichen. Bei einem Radienquotient von 0.5 und größer ist in dem Sinne keine lokale Selektion mehr vorhanden, die `Isolation durch Distanz' ist verschwindend klein.
Für die Auswahl der zu verwendenden Nachbarschaften und deren Vergleich untereinander ist die Angabe der Selektionsintensität in der Population interessant und der Radienquotient bildet einen ersten Anhaltspunkt. Weitere Untersuchungen für allgemein definierte Nachbarschaften und Anordnungen beliebiger Ausdehnung müssen noch durchgeführt werden.
Die in Unterabschnitt 4.4.2, ab S. vorgestellte allgemeine Beschreibung von Nachbarschaften sollte als Grundlage für zukünftige Untersuchungen mit dem lokalen Modell verwendet werden.
Diese Dokument ist Teil der Dissertation von Hartmut Pohlheim
"Entwicklung und systemtechnische Anwendung Evolutionärer Algorithmen".
This document is part of the .
The is not free.
© Hartmut Pohlheim, All Rights Reserved,
(hartmut@pohlheim.com).