7.2.1 Kurzbeschreibung des Systems
7.2.2 Symmetrieeigenschaften der Rückführungsmatrizen
7.2.3 Zielfunktion für die Optimierung
7.2.4 Verwendetes Optimierungsverfahren
7.2.5 Einbringen von problemspezifischem Wissen
7.2.6 Standardlösung für die lineare Zustandsrückführung
7.2 Optimierung eines Gleichstrom-Stellers |
In diesem Abschnitt wird die Optimierung eines Gleichstrom-Stellers (Chopper) beschrieben. Aufgabe des Gleichstrom-Stellers ist es, elektrische Energie aus einer Gleichspannungsleitung mit veränderlicher Spannung auf Zwischenkreise mit konstanter Spannung umzusetzen. Diese Spannung wird von zusätzlichen Invertern verwendet, um die Motoren eines Systems zu speisen. Hier werden diese Motoren und Inverter nur bezüglich ihrer entsprechenden Belastung des Zwischenkreises betrachtet.
In [BEL95] wurde eine Methode zum Entwurf einer Regelung des Gleichstrom-Stellers vorgestellt. Diese Methode beruht auf einer linearen Zustandsrückführung. Durch eine vom Arbeitspunkt abhängige Interpolation zwischen mehreren Parametersätzen für die Zustandsrückführung konnte eine weitere Verbesserung des Systemverhaltens erreicht werden.
Es blieben allerdings Fragen offen, die insbesondere die Güte der entworfenen Regelungen für extreme Einsatzbereiche (schnelles Durchfahren des Arbeitsbereiches) betreffen. Neben der Optimierung der linearen Zustandsrückführung wurde deshalb auch die Verwendung einer quadratischen Zustandsrückführung vorgeschlagen. Für die quadratische Zustandsrückführung gibt es aber keine systematischen Entwurfsverfahren.
Zur Bestimmung der Parameter der quadratischen Zustandsrückführung und der linearen Zustandsrückführungen mit der neuen Zielfunktion werden Evolutionäre Algorithmen eingesetzt.
7.2.1 Kurzbeschreibung des Systems |
Der Gleichstrom-Steller (Chopper) ist ein nichtlineares System 8. Ordnung. Es ist ungedämpft und die Dynamik der Zustände ist stark miteinander gekoppelt.
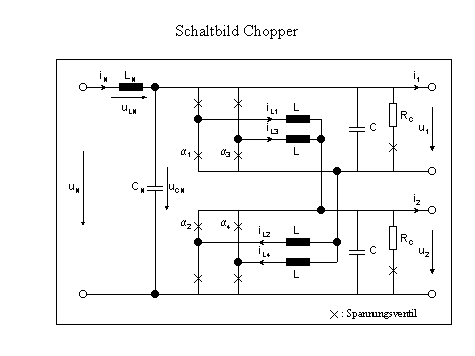
Abbildung 7-11: Schaltbild des Gleichstrom-Stellers (Chopper)
Das System wurde durch zwei weitere Zustände v1 und v2 (Integral der Abweichung der Ausgangsspannungen u1 und u2 von ihren Referenzwerten u10 und u20) erweitert, so daß ein System 10. Ordnung vorliegt. Daraus ergeben sich die folgenden Vektoren für Zustands-, Stell- und Störgrößen:
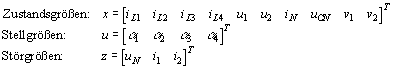 (7-4)
(7-4)
Hauptaufgabe des zu entwerfenden Reglers ist, die Ausgangsspannungen u1 und u2 konstant zu halten. In mehreren Arbeiten (u.a. [BEL95]) wurde gezeigt, daß durch eine Zustandsrückführung solche Systeme behandelt werden können.
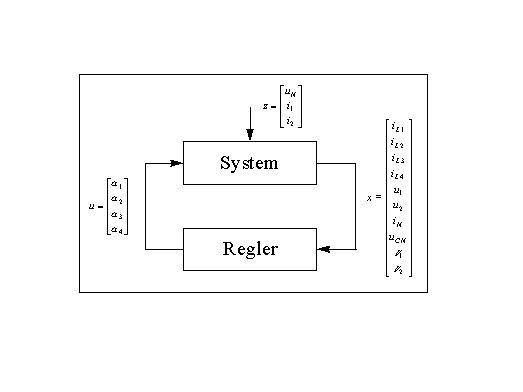
Abbildung 7-12: Struktur der Zustandsrückführung des Choppers
Tabelle 7-1 zeigt eine Übersicht der Parameter, die für die Simulation und Bewertung der Ergebnisse benutzt wurden.
Bezeichnung |
Zeichen |
Wert |
Kapazität der Zwischenkreiskondensatoren |
C |
|
Kapazität des Netzfilterkondensators |
CN |
|
Induktivität der Stellerdrosseln |
L |
|
Induktivität der Netzfilterdrossel |
LN |
|
Soll-Netzspannung |
UN |
3000 V |
Soll-Ausgangsspannung für beide Stränge |
UD0 |
2800 V |
Nennausgangsleistung je Strang |
PN |
1.3 MW |
Abtastzeit |
TA |
0.002 s |
Simulationszeit |
Tsim |
0.5 s |
Tabelle 7-1: Bezeichnung der Parameter des Gleichstrom-Stellers
Eine umfassende Beschreibung des Gleichstrom-Stellers findet sich in [BEL95].
Für die lineare Rückkopplung der Zustände ergibt sich mit der Zustandsrückführung KLin folgende Reglergleichung:
![]() (7-5)
(7-5)
Daraus ermittelt sich die Dimension der Koeffizientenmatrix der linearen Zustandsrückführung KLin zu 4×10. Damit hat die Zielfunktion bei der Optimierung der linearen Zustandsrückführung 40 Parameter.
Die lineare Zustandsrückführung arbeitet gut, wenn der Betriebsbereich langsam durchfahren wird (z.B. Lastrampe).
Für ein schnelles Durchfahren des Betriebsbereiches (z.B. Lastabwurf, Reversieren der Last, asymmetrische Belastungen) war ein besseres Verhalten wünschenswert. Deshalb wurde die Verwendung eines nichtlinearen Reglers vorgeschlagen, der eine quadratische Rückkopplung der Zustände realisiert. Dieser Regler ist möglicherweise für die nichtlineare Struktur des Systems besser geeignet. Außerdem enthält die quadratische Rückkopplung die lineare Rückkopplung als Spezialfall.
Für die quadratische Rückkopplung der Zustände ergibt sich folgende Reglergleichung:
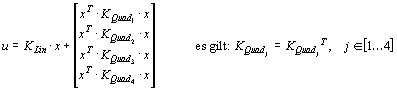 (7-6)
(7-6)
Die Matrix KLin beschreibt den linearen Teil der Zustandsrückführung und hat die Dimension 4×10. Die Matrizen KQuad1-KQuad4 beschreiben den quadratischen Anteil. Jede der Matrizen KQuad1-KQuad4 hat die Dimension 10×10, ist symmetrisch und hat deshalb 55 unabhängige Elemente, insgesamt 4×55=220. Daraus ergeben sich für die quadratische Zustandsrückführung 40+220=260 Elemente. Die Zielfunktion hat damit bei der Optimierung 260 einzustellende Parameter.
7.2.2 Symmetrieeigenschaften der Rückführungsmatrizen |
In [BW96] wurden Untersuchungen zu den Symmetrieeigenschaften von zu regelnden Systemen durchgeführt. Oftmals sind in Systemen Symmetrien der internen Struktur vorhanden. Dies ist auch bei dem hier untersuchten Gleichstrom-Steller der Fall, siehe Abbildung 7-11. Der für ein solches System entworfene Regler sollte diese symmetrischen Eigenschaften ausnutzen. Dadurch könnte die Anzahl der Reglerparameter deutlich verringert werden. Die erarbeiteten Erkenntnisse wurden in [BW96] auf den in diesem Bericht behandelten Gleichstrom-Steller angewendet. Die folgenden Unterabschnitte zeigen die Ergebnisse der Anwendung der Symmetrieeigenschaften des Systems auf die Reglerparameter.
Unter Ausnutzung von 3 Symmetrien ergeben sich die Parameter des symmetrischen Reglers KLin zu:
Zur Betonung ist jedes erste Auftreten eines Parameters fett hervorgehoben, ein wiederholtes Auftreten wird durch eine kursive Formatierung verdeutlicht. Nur die Parameter der ersten Zeile mit Ausnahme des 4. Parameters treten in der symmetrischen linearen Zustandsrückführung auf. Durch die Symmetrien verringerte sich die Anzahl der unabhängigen Parameter der Zustandsrückführung von 40 auf 9 Parameter.
Für den linearen Teil der quadratischen Zustandsrückführung gelten dieselben Ergebnisse wie für die lineare Zustandsrückführung aus Gleichung 7-7.
Beim quadratischen Teil können 3 Symmetrien ausgenutzt werden. Es treten in den Matrizen KQuad1-KQuad4 nur Parameter aus Matrix KQuad1 auf und in dieser selbst nur 46 unabhängige Parameter. Die symmetrische quadratische Zustandsrückführung hat damit nur noch 9+46=55 unabhängige Parameter, eine deutliche Reduzierung gegenüber den ursprünglich 260 Parametern.
7.2.3 Zielfunktion für die Optimierung |
Für die Arbeit des Evolutionären Algorithmus ist die Zielfunktion der einzige Anhaltspunkt. Gerade bei komplizierteren Zielfunktionen ist eine richtige Definition der Zielfunktion ein schwieriges Unterfangen. Oftmals wird erst bei den ersten Optimierungen festgestellt, daß die anfängliche Definition nicht die erhofften Ergebnisse produziert.
Die Zielfunktionen wurden am Institut für Antriebstechnik und Leistungselektronik der Daimler Benz Forschung in Berlin entwickelt und implementiert sowie nach der Vorstellung erster Ergebnisse verändert bzw. erweitert.
Zuerst wurden Optimierungen der linearen Zustandsrückführung durchgeführt. An dieser konnte getestet werden, welche Ergebnisse durch eine Optimierung erreicht werden und ob diese Ergebnisse die erhoffte Verbesserung zeigen. Die anfangs als ausreichend angesehene erste Zielfunktion zeigte sehr schnell ihre Mängel. Durch die fehlende Bewertung einiger Größen bzw. Eigenschaften (z.B. Gleichverteilung der Lastströme) wurden unerwünschte Ergebnisse erreicht. Die erste Zielfunktion entsprach damit nicht den Vorstellungen. Daraufhin entstand die zweite Zielfunktion, die diese Größen mit einbezog. Mit den Erkenntnissen aus diesen Arbeiten wurde eine Überarbeitung der Zielfunktion vorgenommen, die alle relevanten Größen beinhaltet. Zusätzlich war die Überarbeitung der Zielfunktion notwendig geworden, da die Simulation des Choppers stark ausgebaut wurde und dadurch den technischen Realitäten besser entsprach. Diese Zielfunktion wird im folgenden mit ihren Komponenten beschrieben.
Die Zielfunktion kombiniert die Bewertung der folgenden Größen:
Berechnung der normierten Abweichung der Strangspannungen u1 und u2 von der Sollausgangsspannung UD0 und der Spannung uCN von der Netzspannung UN unter Beachtung von uLN :
Durch die Wahl von ExpoU können die Differenzen mit unterschiedlichen Potenzen berechnet werden (höhere Potenzen bewerten große Differenzen stärker als kleine Differenzen).
Berechnung des induktiven Spannungsabfalls uLN über LN, der in die Ermittlung der Referenzspannung für uCN bei der Berechnung von DiffuCN in Gleichung 7-8 eingeht:
![]() (7-9)
(7-9)
Die Spannungen u1, u2 und uCN werden über den Simulationszeitraum und für jedes Szenario unterschiedlich stark gewichtet. Dadurch werden bestimmte Bereiche eines jeden Szenarios deutlich stärker bewertet, andere Zeitbereiche dafür weniger.
Die normierten Differenzen werden durch Summenbildung integriert und die Maxima der Differenzen addiert (Integration des Regelfehlers):
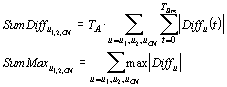 (7-10)
(7-10)
Berechnung der Summe der normierten Maxima der Lastströme iL1-iL4:
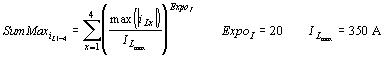 (7-11)
(7-11)
Die normierten Lastströme iL1-iL4 werden durch Summenbildung integriert:
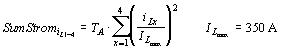 (7-12)
(7-12)
Berechnung der normierten Differenz zwischen den parallelen Zweigen iL1/iL2 und iL3/iL4:
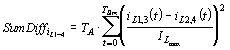 (7-13)
(7-13)
Zum Abschluß erfolgt eine logarithmische Normierung der Summe aller zu bewertenden Größen:
Die Wichtungsfaktoren W wurden für jede der Größen so festgelegt, daß die Größenordnung der einzelnen Werte aufeinander abgestimmt ist. Die addierte Zahl 1.01 stellt sicher, daß der Zielfunktionswert immer größer null ist.
Mit Gleichung 7-14 wird der Zielfunktionswert für ein Szenario berechnet. Die Wichtungsfaktoren W sind für jedes Szenario einzeln festgelegt, um die auch zwischen Szenarien sehr unterschiedlichen Größenordnungen der einzelnen Größen der Zielfunktion aufeinander abzustimmen. (Alternativ dazu könnte eine mehrkriterielle Bewertung verwendet werden. Allerdings ist diese nur wenig besser zu überblicken, da Zielbereiche (goals) für die einzelnen Werte nicht direkt definierbar sind. Ein Pareto-Ranking allein ist nicht ausreichend.)
Wenn Optimierungen über mehrere Szenarien gleichzeitig durchgeführt werden, so wird als Zielfunktionswert die einfache Summe der Gütewerte aller benutzten Szenarien verwendet. Eine Wichtung der einzelnen Szenarien fand schon bei der Festlegung der Wichtungsfaktoren W in Gleichung 7-14 statt.
Diese Zielfunktion wurde für alle weiteren Arbeiten verwendet. Eine Auswahl der Ergebnisse verschiedener Optimierungen ist in den folgenden Unterabschnitten dargestellt.
7.2.4 Verwendetes Optimierungsverfahren |
Für die Optimierung der Zustandsrückführung des Choppers wurde mit zwei Verfahren gearbeitet. Das erste Verfahren ist ein Evolutionärer Algorithmus mit mehreren Unterpopulationen, die jede mit einem anderen Satz von Strategieparametern arbeitet (Anwendung verschiedener Strategien, siehe Abschnitt 4.5, ab S.). Im weiteren Verlauf wurden Optimierungen mit einem Evolutionären Algorithmus durchgeführt, der zur Mutation den Mutationsoperator einer Evolutionsstrategie nach Unterabschnitt 3.4.2 verwendet.
Evolutionärer Algorithmus mit Unterpopulationen und verschiedenen Strategien (MSEA - multiple strategy evolutionary algorithm):
Evolutionärer Algorithmus mit Evolutionsstrategie als Mutationsoperator (ESA - evolutionary strategy algorithm):
Der Vorteil des MSEA liegt in seiner größeren Robustheit bei der Suche. Der ESA ist deutlich schneller im Finden eines Minimums, läuft dabei aber eher Gefahr, in einem lokalen Minimum zu landen. Der MSEA ist deshalb besser für die grobe Suche geeignet, wobei er durch die Verwendung verschiedener Strategien am Ende auch gut bei der lokalen Suche ist. Der ESA ist schneller, sucht aber nur lokal. Daher wird ESA für die abschließende Suche zum sehr feinen Einstellen der Parameter verwendet.
7.2.5 Einbringen von problemspezifischem Wissen |
Erste Versuche mit einer zufälligen Initialisierung der Anfangspopulation zeigten recht schnell, daß die Evolutionären Algorithmen mit vernünftigem Aufwand keine gute Lösung finden. Daher wurde das problemspezifische Wissen, das vom System bekannt ist, verwendet und in die Initialisierung der Anfangspopulation sowie die Definition des Suchbereiches eingebracht.
Als Grundlage diente die Standardlösung (lineare Zustandsrückführung einfach), die in Abschnitt 7.2.6 erläutert wird. Die damit erhaltenen Parameter einer schon recht guten Zustandsrückführung dienten zum Eingrenzen eines vielversprechenden Initialisierungsbereiches und zum Festlegen des Suchbereiches für jeden Parameter.
Durch dieses Vorgehen konnten mehrere Dinge erreicht werden:
Noch wichtiger für die Optimierung ist aber die Ausnutzung des Wissens über vorhandene Symmetrien, siehe Unterabschnitt 7.2.2, S.. Dies verringert nicht nur die Anzahl der zu optimierenden Parameter. Zusätzlich werden alle Kopplungen zwischen den Parametern aufgelöst, da nur noch voneinander unabhängige Parameter optimiert werden. Nachdem dieses Wissen in den Optimierungsprozeß einbezogen wurde, konnte auf eine spezielle Initialisierung der linearen Zustandsrückführung verzichtet werden. Eine vernünftige Festlegung des Definitionsbereiches jeder Variablen erwies sich als ausreichend. Gute Ergebnisse wurden durch das Ausnutzen der Symmetrieeigenschaften mit relativ geringem Aufwand und großer Sicherheit gefunden.
Die Optimierung der quadratischen Zustandsrückführung, die ohne Einbeziehung der Symmetrieeigenschaften sehr schwer gewesen wäre, wurde jetzt zu einer lösbaren Aufgabe. Für eine Initialisierung des linearen Teils können die Ergebnisse der Optimierungen der linearen Zustandsrückführung genutzt werden. Für den quadratischen Teil war dagegen kein Vorwissen für eine Initialisierung der Parameter vorhanden.
7.2.6 Standardlösung für die lineare Zustandsrückführung |
Obwohl der Chopper eine nichtlineare Struktur hat, kann durch lineare Zustandsrückführung die Regelungsaufgabe gelöst werden. In [BEL95] wurde der Entwurf einer linearen Zustandsrückführung beschrieben (LQR-Entwurf). Dafür wurde ein quadratisches Gütekriterium aufgestellt:
Q und R sind frei wählbare, physikalisch interpretierbare Wichtungsmatrizen. In die Festlegung der Elemente dieser Matrizen kann Wissen über das System einfließen. In [BEL95] ist die Festlegung der Matrizenelemente genauer erläutert. Unter anderem sind die Wichtungsmatrizen so gewählt, daß in der durch LQR-Entwurf berechneten linearen Zustandsrückführung die im Unterabschnitt 7.2.2 beschriebenen Symmetrien bereits enthalten sind. Das Ergebnis des LQR-Entwurfs mit der Zielfunktion in Gleichung 7-15 ist für die gewählten Wichtungsmatrizen die optimale Lösung.
Die für den LQR-Entwurf verwendete Zielfunktion in Gleichung 7-15 unterscheidet sich deutlich von der für die Optimierung mit Evolutionären Algorithmen benutzten Zielfunktion, siehe Unterabschnitt 7.2.3, S.. Beim LQR-Entwurf ist die Struktur der Zielfunktion fest vorgegeben, eine Beeinflussung ist nur durch die Wahl der Wichtungsmatrizen Q und R möglich. Die Zielfunktion für die Optimierung mit Evolutionären Algorithmen hat keine solchen Beschränkungen. Hier können alle Größen aufgenommen werden, die als wichtig erachtet werden. Allerdings ist die Aufstellung einer solchen Zielfunktion oftmals nicht so einfach, wie die Festlegung der Wichtungsmatrizen beim LQR-Entwurf.
Die Ergebnisse des LQR-Entwurfes werden in allen weiteren Untersuchungen als Standardlösung bezeichnet. Dabei muß zwischen zwei Fällen unterschieden werden:
Abbildung 7-13: Ergebnisse der Simulation mit der Standardlösung lineare Zustandsrückführung dreifach, Szenarien 5, 7, 8 und 9
Alle durch die Optimierung mit Evolutionären Algorithmen erreichten Lösungen müssen sich an den Ergebnissen dieser Standardlösungen messen lassen. Die lineare Zustandsrückführung dreifach erreicht bessere Ergebnisse als die einfache Variante. In Abbildung 7-13 werden deshalb die Ergebnisse der Simulation des Systems mit der Standardlösung dreifach gezeigt. Die Ergebnisse dieser Simulation dienten auch zur Festlegung der Wichtungen der einzelnen Größen der Zielfunktion und der einzelnen Szenarien, siehe Gleichung 7-14. Daher sind die Gütewerte der Szenarien bei Verwendung dieser Parameter alle gleich.
Die in Abbildung 7-13 gewählte Form der Darstellung, ein Beispiel für die Visualisierung problemspezifischer Daten, siehe Unterabschnitt 5.4.3, ab S., wird in den folgenden Beispielen immer wieder verwendet. Die grafische Präsentation zeigt auf einen Blick alle notwendigen Informationen.
An dieser Stelle folgen einige Hinweise zu den in den Abbildungen mit den Ergebnissen von Simulationen dargestellten Verläufen und Werten:
Bei der folgenden Auswertung der Ergebnisse der Optimierungen werden jeweils dieselben Szenarien verwendet, die in Abbildung 7-13 dargestellt sind. Ein optischer Vergleich ist dadurch direkt möglich.
7.2.7 Ergebnisse der Optimierung |
Dieser Unterabschnitt zeigt ausgewählte Ergebnisse, die bei den verschiedenen Optimierungen der linearen und quadratischen Zustandsrückführung gefunden wurden. Ziel dieser Arbeiten war, neben der anfänglichen Überprüfung der Zielfunktion, mittels der Optimierung eine bessere Lösung für die lineare Zustandsrückführung gegenüber den bisher verwendeten klassischen Entwurfsverfahren sowie eine Lösung für die quadratische Zustandsrückführung zu finden.
Eine Optimierung der linearen Zustandsrückführung kann in verschiedenen Stufen durchgeführt werden:
Die erste Variante wurde in der Anfangszeit der Arbeit mit dem Chopper verwendet. Durch die Einbeziehung der Symmetrien können aber bessere Ergebnisse erreicht werden, so daß mit der ,,unsymmetrischen" Variante nicht mehr gearbeitet wird. Die Optimierung der linearen symmetrischen Zustandsrückführung einfach kann als Minimalvariante betrachtet werden. Damit sollte nach den Grenzen dieser Zustandsrückführung gesucht werden. Außerdem dienen diese Untersuchungen der späteren Initialisierung des linearen Teil der quadratischen Zustandsrückführung. Die dritte Variante der linearen symmetrischen Zustandsrückführung dreifach ist die aktuell beste bekannte Methode, und mit den Optimierungen sollten weiter verbesserte Varianten gefunden werden.
Für die Optimierung der quadratischen Zustandsrückführung bestehen die folgenden Varianten:
Die erste Variante ist nicht sinnvoll. Die zweite Variante wurde für die ersten Optimierungen der quadratischen Zustandsrückführung genutzt, um den Wertebereich sinnvoller Parameter zu suchen. Für die volle Optimierung der quadratischen Zustandsrückführung wurde nur die dritte Variante verwendet.
Für die Präsentation aller Ergebnisse wird die grafische Darstellung der Simulationsergebnisse zusammen mit den Parametern der optimierten Rückführungsmatrix gewählt. Da eine vollständige grafische Darstellung aller 9 Szenarien zuviel Platz einnimmt, wird jeweils nur eine Auswahl an Szenarien in den jeweiligen Grafiken gezeigt. Am Ende des Unterabschnitts findet sich in Tabelle 7-2 eine Zusammenstellung der Gütewerte für alle Regler und jedes Szenario. Dies erlaubt den Vergleich der Gütewerte für alle Szenarien.
Die Ergebnisse in Abbildung 7-14 wurden durch Optimierung der linearen Zustandsrückführung einfach erreicht. Die Szenarien 1, 2, 4, 5, 6 und 9 wurden für die Optimierung benutzt. Diese 6 Szenarien waren ausreichend zur Repräsentation aller 9 Szenarien. Allerdings durfte keines der 6 Szenarien bei der Optimierung weggelassen werden, da sonst Parameter gefunden wurden, die für die nicht optimierten Szenarien keine sehr guten Ergebnisse brachten.
Zum Vergleich der Zielfunktionswerte für alle Szenarien in Tabelle 7-2 können zwei Bezugsgrößen herangezogen werden:
Im Vergleich zur Standardlösung der linearen Zustandsrückführung einfach ist das Ergebnis gemischt. Die Zielfunktionswerte sind für einige Szenarien etwas schlechter. Dies sind aber meist die Szenarien, die bei der Standardlösung schon sehr gut waren. Dagegen sind alle die Szenarien deutlich besser, die mit der Standardlösung schlecht waren. Besonders deutlich wird dies bei den Szenarien 5 und 6. Über alle Szenarien gesehen ist die optimierte lineare Zustandsrückführung einfach besser als die Standardlösung für diese Zustandsrückführung.
Im Vergleich zur Standardlösung der linearen Zustandsrückführung dreifach ist die optimierte lineare Zustandsrückführung einfach bei den meisten Szenarien schlechter, nur bei Szenario 2, 5, 6, und 8 sind die Gütewerte besser. Ein Blick auf die Simulationsergebnisse der Szenarien in Abbildung 7-14 zeigt, daß das Verhalten der optimierten Zustandsrückführung recht gut ist. Erkennbare Unterschiede zu Abbildung 7-13 sind bei den dargestellten Szenarien nur bei Szenario 8 zu sehen. Die Schwingungen des Systems sind schon nach 0.3s beendet. Kritisch zu bewerten ist das Verhalten bei Szenario 9. Die am Ende schwachen Schwingungen kommen innerhalb der Simulationszeit nicht zur Ruhe.
Abbildung 7-14: Ergebnisse der Simulation mit einer optimierten linearen symmetrischen Zustandsrückführung einfach (Nr. 43), Szenarien 5, 7, 8 und 9 (optimiert mit Szenarien 1, 2, 4, 5, 6 und 9)
In Abbildung 7-15 sind die Ergebnisse einer Optimierung der linearen Zustandsrückführung dreifach dargestellt. Für die Optimierung wurden die Szenarien 1, 2, 4, 5, 6 und 9 verwendet. Die Szenarien 3, 7 und 8 wurden während der gesamten Optimierung nicht benutzt. Trotzdem sind die Ergebnisse auch für diese Szenarien sehr gut.
Ein Vergleich der Gütewerte der dargestellten Szenarien sowie aller Gütewerte in Tabelle 7-2, S., zeigt, daß diese optimierte Zustandsrückführung die besten Gütewerte aller Zustandsrückführungen aufweist. Die Werte liegen für alle Szenarien unter den Werten der als Standardlösung verwendeten linearen Zustandsrückführung dreifach aus Unterabschnitt 7.2.6, S.. Für einige Szenarien sind die Gütewerte deutlich kleiner als die der Standardlösung.
Neben dem Vergleich der Gütewerte sollen wieder die Simulationsergebnisse einiger Szenarien für den Vergleich herangezogen werden. In Abbildung 7-15 sind die vier Szenarien 5, 7, 8 und 9 dargestellt, bei denen sich grafisch Unterschiede zur Standardlösung in Abbildung 7-13, S., ausmachen lassen. Die Unterschiede sind allerdings nur noch im Detail zu finden, da die prinzipiellen Verläufe sehr ähnlich sind. Deshalb wurden einige der erkennbaren Unterschiede in den einzelnen Grafiken mit gestrichelten Kreisen bzw. Ellipsen für eine einfachere Erfassung gekennzeichnet.
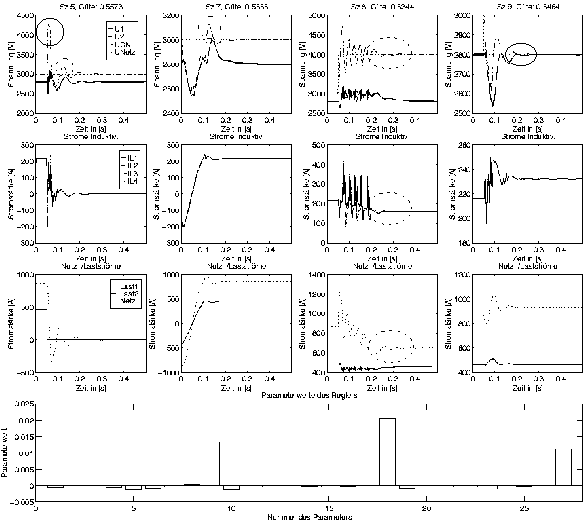
Abbildung 7-15: Ergebnisse der Simulation mit einer optimierten linearen symmetrischen Zustandsrückführung dreifach (Nr. 54), Szenarien 5, 7, 8 und 9 (optimiert mit Szenarien 1, 2, 4, 5, 6 und 9)
Bei Szenario 5 und 7 sind die Ausschläge von UCN geringer. Signifikantere Unterschiede sind in Szenario 8 zu erkennen. In allen 3 Grafiken für Szenario 8 ist zu erkennen, daß die Schwingungen des Systems nach 0.25s beendet sind. Bei der Verwendung der Standardlösung geschah dies erst nach 0.4s. In Szenario 9 kehren die Werte für U1 und U2 nach 0.25s auf den geforderten Wert von 2800V zurück. Mit der Standardlösung konnte dies erst nach 0.4s erreicht werden. Dafür ist in Szenario 9 der positive Maximalwert des Lastströme IL1-IL4 etwas höher.
Ein Ergebnis der Optimierungen der quadratischen symmetrischen Zustandsrückführung ist in Abbildung 7-16 dargestellt. Analog zu den anderen Ergebnisdarstellungen werden die Simulationsergebnisse für die Szenarien 5, 7, 8 und 9 gezeigt. Für die Optimierung wurden die Szenarien 1, 2, 4, 5, 6 und 9 verwendet.
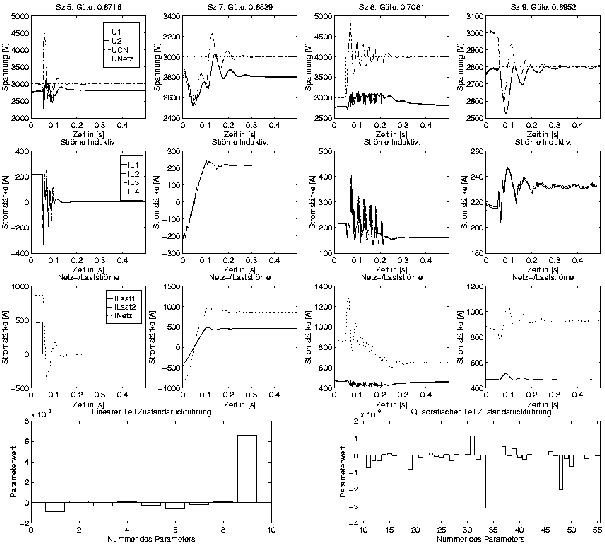
Abbildung 7-16: Ergebnisse der Simulation mit einer optimierten quadratischen symmetrischen Zustandsrückführung (Nr. 65), Szenarien 5, 7, 8 und 9 (optimiert mit Szenarien 1, 2, 4, 5, 6 und 9)
Ein Blick auf die Simulationsergebnisse in Abbildung 7-16 sowie die Gütewerte in Tabelle 7-2 zeigt, daß die Gütewerte für fast alle Szenarien besser als für die Standardlösung der linearen Zustandsrückführung dreifach sind. Nur bei drei Szenarien (1, 4 und 8) sind die Gütewerte etwas größer. Die Verbesserungen gegenüber der Standardlösung zeigen sich auch in den Simulationsergebnissen.
Wird dagegen ein Vergleich mit den Gütewerten der optimierten linearen Zustandsrückführungen einfach und dreifach durchgeführt, dann sehen die Ergebnisse nicht mehr so positiv aus. Die Ergebnisse der optimierten linearen Zustandsrückführung einfach liegen in derselben Größenordnung, wie die optimierte quadratische Zustandsrückführung. Die Simulationsergebnisse sind denen der optimierten linearen Zustandsrückführung einfach in Abbildung 7-14 sehr ähnlich, eine Verbesserung ist nicht zu erkennen. Ein Blick auf den linearen Teil der Parameter beider Zustandsrückführungen zeigt, daß diese Werte für beide Ergebnisse fast identisch sind.
Im Vergleich zur optimierten linearen Zustandsrückführung dreifach sind die Gütewerte der quadratischen Zustandsrückführung für alle Szenarien schlechter. Dies zeigt sich in der grafischen Darstellung der Simulationsergebnisse nicht so deutlich, da die Ergebnisse trotzdem gut sind. Aber die erhofften weiteren Verbesserungen durch den Einsatz einer quadratischen Zustandsrückführung konnten nicht bestätigt werden. Die optimierte quadratische Zustandsrückführung zeigt keine erkennbaren Vorteile gegenüber der optimierten linearen Zustandsrückführung einfach.
Ein Vergleich der Optimierungen für die verschiedenen Zustandsrückführungen mit den Standardlösungen wird in Tabelle 7-2 gegeben. In der Tabelle sind die Zielfunktionswerte für jedes der neun zur Verfügung stehenden Szenarien und die entsprechenden Zustandsrückführungen aufgeführt (kleinere Werte sind besser).
Zustandsrückführung |
Sz. 1 |
Sz. 2 |
Sz. 3 |
Sz. 4 |
Sz. 5 |
Sz. 6 |
Sz. 7 |
Sz. 8 |
Sz. 9 |
Sum |
Standard linear einfach: keine Abb. |
0.7048 |
0.6314 |
0.7094 |
0.7006 |
6.1079 |
1.3444 |
0.7112 |
0.7466 |
0.6957 |
12.352 |
Standard linear dreifach: Abb.7-13 |
0.6981 |
0.6981 |
0.6981 |
0.6981 |
0.6981 |
0.6981 |
0.6981 |
0.6981 |
0.6981 |
6.283 |
optim. linear sym. einfach: Abb.7-14 |
0.7383 |
0.6569 |
0.7088 |
0.7252 |
0.6454 |
0.5481 |
0.7022 |
0.5841 |
0.7175 |
6.026 |
optim. linear sym. dreifach: Abb.7-15 |
0.6593 |
0.6584 |
0.6151 |
0.6772 |
0.5573 |
0.5589 |
0.5665 |
0.6344 |
0.6464 |
5.573 |
optim. quadratisch. sym.: Abb.7-16 |
0.7039 |
0.6651 |
0.6801 |
0.7016 |
0.6716 |
0.5647 |
0.6839 |
0.7081 |
0.6951 |
6.074 |
Tabelle 7-2: Vergleich der Gütewerte für jedes Szenario für alle in Unterabschnitt 7.2.7 vorgestellten Optimierungsergebnisse sowie die Standardlösungen aus Unterabschnitt 7.2.6
Die ersten beiden Zeilen mit den Werten für die Standardlösung der linearen Zustandsrückführung einfach und die Standardlösung der linearen Zustandsrückführung dreifach dienen als Vergleichs- bzw. Ausgangspunkt. Die lineare Zustandsrückführung einfach ist die Minimalvariante in Bezug auf die Anzahl der Parameter (9 Parameter bei Verwendung der symmetrischen Zustandsrückführung). Die lineare Zustandsrückführung dreifach stellt die bisher eingesetzte Lösung dar. An diesen beiden Standardlösungen, speziell der linearen Zustandsrückführung dreifach, müssen sich alle Ergebnisse der Optimierungen mit Evolutionären Algorithmen messen.
Durch die Optimierung konnten die Lösungen für die lineare Zustandsrückführung einfach und dreifach jeweils deutlich verbessert werden. Für die lineare Zustandsrückführung dreifach wurden Lösungen gefunden, die für alle Szenarien bessere Zielfunktionswerte aufweisen, als die bisher beste bekannte Standardlösung.
Für die quadratische Zustandsrückführung konnten Parameter ermittelt werden. Diese Lösungen zeigen aber keine deutliche Verbesserung gegenüber der optimierten linearen Zustandsrückführung einfach. Gegenüber der linearen Zustandsrückführung dreifach sind sie sogar schlechter. Es bleibt eine offene Frage, ob es nicht möglich ist, mit einer quadratischen Zustandsrückführung bessere Lösungen zu erreichen, oder ob solche Lösungen nur nicht gefunden wurden.
7.2.8 Zusammenfassung Chopper |
In diesem Abschnitt wurde die Optimierung der Zustandsrückführung für einen Gleichstrom-Steller mit Evolutionären Algorithmen vorgestellt. Ausgangspunkt für die Arbeiten waren zwei mit Standardverfahren entworfene Zustandsrückführungen: eine lineare Zustandsrückführung (einfach) und eine zwischen drei Arbeitspunkten interpolierende lineare Zustandsrückführung (dreifach).
Durch eine Optimierung beider Zustandsrückführungen mit Evolutionären Algorithmen konnten jeweils bessere Ergebnisse, verglichen mit den Standardlösungen, erreicht werden. Die optimierte dreifache lineare Zustandsrückführung zeigte sehr gute Ergebnisse in den Simulationen der neun verwendeten Szenarien.
Für eine weitere Verbesserung des Verhaltens des Gleichstrom-Stellers war eine quadratische Zustandsrückführung vorgeschlagen worden. Die Parameter dieser Zustandsrückführung wurden mit Evolutionären Algorithmen optimiert. Vergleiche mit den Ergebnissen anderer Optimierungsmethoden waren nicht möglich, da für diese Art von Zustandsrückführung keine geschlossenen Entwurfsverfahren zur Verfügung stehen.
Im Ergebnis der Optimierungen der quadratischen Zustandsrückführung konnten Verbesserungen gegenüber den Standardlösungen erreicht werden. Die optimierte quadratische Zustandsrückführung war allerdings nur so gut, wie die optimierte lineare Zustandsrückführung einfach. Es konnten keine Verbesserungen gegenüber der optimierten linearen Zustandsrückführung dreifach erreicht werden. Beim Vergleich der erreichten Zielfunktionswerte für die einzelnen Szenarien ist die lineare Zustandsrückführung dreifach besser als die quadratische Zustandsrückführung.
Welche der optimierten Lösungen letztendlich eingesetzt wird, ist eine Entscheidung, die von den Fachleuten des entsprechenden Problems getroffen werden muß. Durch die Optimierung mit Evolutionären Algorithmen konnten Lösungen erarbeitet werden, die besser als die bisher bekannten sind. Außerdem wurden Lösungen für eine Aufgabe gefunden, die mit geschlossenen Verfahren nicht lösbar ist.
Bei der Optimierung des Gleichstrom-Stellers zeigte sich ein Vorteil des Einsatzes Evolutionärer Algorithmen deutlich. In der Definition der Zielfunktion konnten alle für den Anwender relevanten Größen und Meßwerte zur Bewertung des Verhaltens des Systems berücksichtigt werden. Außerdem ließ sich das vorhandene problemspezifische Wissen ohne großen Aufwand direkt in die Suche einbinden, was zu einer deutlichen Verbesserung der Ergebnisse der Optimierung und der benötigten Rechenzeit führte.
Diese Dokument ist Teil der Dissertation von Hartmut Pohlheim
"Entwicklung und systemtechnische Anwendung Evolutionärer Algorithmen".
This document is part of the .
The is not free.
© Hartmut Pohlheim, All Rights Reserved,
(hartmut@pohlheim.com).