7.1.2 Kurzbeschreibung des Gewächshausklimamodells
7.1.3 Repräsentation der Individuen und Zielfunktion
7.1.4 Einbeziehung problemspezifischen Wissens
7.1.5 Ergebnisse: Optimale Steuerung für durchschnittliche Tage
7.1.6 Ergebnisse: Optimale Steuerung bei veränderten Preisen
7.1.7 Ergebnisse: Optimale Steuerung unter Verwendung realer Wetterdaten
7.1 Steuerung des Klimas in einem Gewächshaus für die Gemüseproduktion |
Die Verwendung Evolutionärer Algorithmen für die Berechnung der optimalen Steuerung eines komplexen dynamischen Systems wird am Beispiel der Steuerung der Zustandsgrößen in einem Gewächshaus dargestellt. Grundlage ist ein integriertes Modell (Gewächshausklima, Wachstum und Transpiration des Pflanzenbestandes) für die Vorhersage von Temperatur, Luftfeuchtigkeit und CO2-Konzentration im Gewächshaus in einem Zeitbereich von 15-60 Minuten (Kurzfristmodell).
Die Optimierung der Steuerung des Gewächshausklimas wurde mit dem Ziel einer Maximierung des Gewinns unter Berücksichtigung von Beschränkungen (z.B. Verhinderung von Streß für die Pflanzen) durchgeführt. Durch die Einbeziehung von aufgabenspezifischem Wissen in den Evolutionären Algorithmus gelang es, wesentlich schneller zu besseren Ergebnissen zu gelangen, als dies mit einem normalen Evolutionären Algorithmus möglich war. Es werden Ergebnisse der Optimierung für durchschnittliche Tage verschiedener Jahreszeiten, bei sich ändernden Preisen und unter Verwendung realer Wetterdaten gezeigt.
7.1.1 Einleitung |
Die Effektivität der Pflanzenproduktion im Gewächshaus hängt entscheidend von der Einstellung optimaler klimatischer Wachstumsbedingungen zur Erzielung hoher Erträge bei niedrigem Aufwand, guter Qualität und geringer Umweltbelastung ab. Um dies zu erreichen, müssen gleichzeitig mehrere Einflußgrößen wie Temperatur, Luftfeuchte und CO2-Konzentration in jedem Zeitpunkt entsprechend vorgegebener Kriterien durch Heizen, Lüften, CO2-Zufuhr u.a. optimal gesteuert werden. Da dieser sich ständig ändernde optimale Zustand in der gesamten Vegetationsperiode einzuhalten ist, ergibt sich eine hochdimensionale Optimierungsaufgabe.
Auf der Basis nichtlinearer Optimierungen mit Ertragsmodellen (Gurke, Tomate) wurden für Diskretisierungsintervalle von mehreren Tagen beispielsweise in [Arn87], [Mar90] und [Sch85] Lösungen vorgestellt. Es handelt sich hierbei um dynamische Langfriststeuerungen, die durch entsprechende Steuerungen im Kurzfristbereich (Minuten, Stunden) zu ergänzen sind. Die Langfriststeuerung ist dabei die übergeordnete Steuerung, welche den pflanzenbaulich zulässigen Steuerungsbereich für die untergeordnete Kurzfriststeuerung vorgibt.
In diesem Abschnitt wird eine auf einem einfachen Modell des Gewächshausklimas [Hei96] beruhende Optimierung der Temperatur, Luftfeuchte und CO2-Konzentration im Kurzfristbereich (15-60 Minuten) durch Anwendung Evolutionärer Algorithmen vorgestellt.
7.1.2 Kurzbeschreibung des Gewächshausklimamodells |
Das Gewächshausklimamodell, Abbildung 7-2, beschreibt die Abhängigkeit der Temperatur, der Luftfeuchte und der CO2-Konzentration im Gewächshaus von den Stellgrößen sowie den mikrometeorologischen Bedingungen im Freien mit einem System von drei nichtlinearen Differentialgleichungen 1. Ordnung.
Die drei Differentialgleichungen des Modells sind die Bilanzgleichungen im Gewächshausinnenraum für 1) Energie, Gleichung A3-1, 2) Wasserdampf, Gleichung A3-2, und 3) Kohlendioxid, Gleichung A3-3.
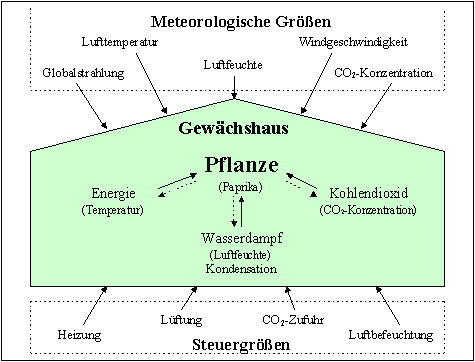
Abbildung 7-2: Schema des Gewächshausklimamodells
Das Gewächshausklima kann durch 4 Stellgrößen beeinflußt werden: 1) Heizung, Q [W/m²], 2) Lüftung, LR [m³/m²], 3) CO2-Zufuhr, W [g/(m²·h)], und 4) Luftbefeuchtung, RM [g/(m²·h)].
Die zu messenden mikrometeorologischen Bedingungen im Freien sind 1) Globalstrahlung, IGLOB [W/m2], 2) Lufttemperatur außen, TEMA [°C], 3) Luftfeuchte außen, FA [% r.F.], 4) CO2-Konzentration außen, CA [ppm] und 5) Windgeschwindigkeit, U [m/s].
Im Gewächshausmodell wird nur ein Kompartiment betrachtet (Gewächshausinnenraum mit Pflanzenbestand). Deshalb müssen neben den Bedingungen im Freien weitere Eingangsgrößen berücksichtigt werden: 1) Temperatur der Bodenoberfläche, TEMB [°C], und 2) Temperatur der Gewächshaushülle, TEMG [°C].
Die Pflanzen im Gewächshaus werden durch zwei Größen modelliert: 1) CO2-Gaswechsel, Gleichung A3-4, und 2) Transpiration, Gleichung A3-5. Aus dem CO2-Gaswechsel wird die Biomasseproduktion berechnet, Tabelle A3-1. Für die Simulationen wurden die Modelle für Paprika verwendet [Hei97].
Die in den Bilanzgleichungen verwendete Temperaturgröße ist durch die spezifische Wärmekapazität von Luft und Pflanzen (Volumen pro Grundfläche und Wasseräquivalent des Pflanzenbestandes) im Gewächshaus definiert und stellt damit ein Mittel aus Luft- und Pflanzentemperatur dar.
Die Berechnungen mit dem Modell benutzen eine Reihe von physikalischen Konstanten, Gewächshausparametern und -hilfsgrößen sowie Koeffizienten für die Darstellung der Transpiration und des CO2-Gaswechsels durch Modelle und Pflanzenbestandsparameter ([Hei96], [PH96a]).
Eine ausführlichere Darstellung des Gewächshausklimamodells und der Pflanzenmodelle wird in Abschnitt A.3, S., sowie in [Hei96] und [Hei97] gegeben.
Für die Optimierung sind insbesondere das Zusammenspiel und die gegenseitigen Abhängigkeiten der verschiedenen Größen und ihre Auswirkungen auf die Bewertung, hier den Gewinn, wichtig. In Abbildung 7-3 sind diese Abhängigkeiten der Zielfunktion dargestellt. Im Gewächshaus befinden sich die Pflanzen. Deren Wachstum wird durch das Klima im Gewächshaus und einen Teil der äußeren Wetterbedingungen beeinflußt. Das Gewächshausklima wiederum wird durch die äußeren Wetterbedingungen, die Steuerung und die vorgegebenen Beschränkungen beeinflußt. Zusätzlich wirken auch die Pflanzen auf das Gewächshausklima zurück. Aus der Biomasseproduktion der Pflanzen kann ein Ertrag errechnet werden, der vermindert um die Aufwendungen für die Steuerung den Gewinn ergibt. Diese immer noch vereinfachende Übersicht zeigt recht deutlich die komplexen Zusammenhänge und Abhängigkeiten der Größen des Gewächshausklimamodells.
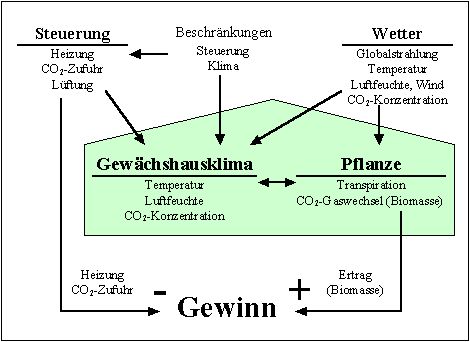
Abbildung 7-3: Abhängigkeiten der Zielfunktion
7.1.3 Repräsentation der Individuen und Zielfunktion |
Jedes Individuum im Evolutionären Algorithmus repräsentiert die Steuerung für eine Simulationsperiode. Wie in Abschnitt 7.1.2, S. , gezeigt wurde, kann das Gewächshausklima durch 4 Größen gesteuert werden. Im Moment werden 3 Größen verwendet: Heizung, Lüftung und CO2-Zufuhr. Die Luftbefeuchtung wird zur Zeit nicht verwendet und ist die gesamte Zeit auf 0 gesetzt.
Die Steuerungen werden zu äquidistanten Zeitpunkten diskretisiert. Für die Simulation wird ein Halteglied 1. Ordnung verwendet, um Werte der Steuerungsgrößen zwischen den Diskretisierungspunkten zu erhalten. Die Anzahl der Variablen kann mittels Gl. 7-1 berechnet werden:
Ein Steuerungsschritt alle 15 Minuten ist für die Simulation klein genug und hält gleichzeitig die Anzahl der Variablen so klein wie vertretbar. Damit ergibt sich, daß für eine Simulationszeit von 4 Stunden ein Individuum aus 51 Variablen besteht.
Um die Anzahl der Variablen und die Optimierungszeiten handhabbar zu halten, wird normalerweise eine Simulationsperiode von 4 Stunden verwendet. Zur Optimierung längerer Perioden wird die Optimierung in Abschnitte von 4 Sunden unterteilt. Die Endzustände einer Simulation bzw. Optimierung dienen dann als Startwerte für die folgende Periode. Damit ist es möglich, selbst sehr lange Simulationszeiträume auf Standardhardware (PC Pentium-120, 32 MB RAM) zu berechnen. Sobald leistungsfähigere Hardware zur Verfügung steht, kann die Simulationsperiode entsprechend verlängert werden.
Die im Modell verwendete Zielfunktion, Cost, Gleichung 7-2, dient zur Maximierung des Gewinns, Gleichung A3-6, unter der Bedingung der Erfüllung der Beschränkungen, siehe Abschnitt A.3.4, S.. Um die Einhaltung der Beschränkungen zu erreichen, wird den Individuen bei Verletzung der Beschränkungen ein Bestrafungswert (Penalty) zugewiesen. Da bei der Optimierung mit einer Minimierung gearbeitet wird, muß in Gleichung 7-2 der Gewinn mit -1 multipliziert werden.
Für die Bestrafungsfunktion Penalty, Gleichung 7-3, kommt eine gewichtete Summe zur Anwendung. Val entspricht entweder einer der Zustandsvariablen des Gewächshausklimas oder einer der Steuerungsgrößen. Constr ist die jeweils dazugehörende Beschränkung. Durch Wahl der Gewichte W kann die Wichtigkeit der Einhaltung dieser Beschränkung definiert werden.
Die Verwendung einer gewichteten Summe zur Berechnung des Bestrafungswertes in Gleichung 7-3 gewährleistet, daß Lösungen mit einer stärkeren Verletzung der Beschränkungen einen höheren Bestrafungswert und Individuen mit einer geringeren Verletzung der Beschränkungen einen kleineren Bestrafungswert erhalten. Dadurch sind Lösungen, welche die Beschränkungen verletzen, nicht einfach schlecht, sondern es gibt eine Reihenfolge unter diesen Lösungen. Dies ist besonders dann wichtig, wenn gute Lösungen sehr nah an den Beschränkungen liegen bzw. leichte Verletzungen der Beschränkungen noch tolerierbar sind. Bei der Optimierung der Steuerung des Gewächshausklimas ist dies für mehrere der Beschränkungen der Fall.
7.1.4 Einbeziehung problemspezifischen Wissens |
Für die Steuerung des Gewächshausklimas gibt es Vorwissen, das in die Optimierung einbezogen werden kann und sollte. Dieses problemspezifische Vorwissen kann in zwei Bereiche unterteilt werden:
Aus der Optimierung der Gewächshausklimasteuerung unter Verwendung durchschnittlicher Tage, siehe Unterabschnitt 7.1.5, ab S., ergeben sich Steuerstrategien für die jeweiligen Monate, die auf den durchschnittlichen Klimadaten basieren. Diese Strategien für die Steuervariablen als Ergebnis von Optimierungen bilden eine Grundlage für die Initialisierung der Anfangspopulation.
Für die Optimierung unter Verwendung realer Wetterdaten, siehe Unterabschnitt 7.1.7, ab S., wurde jeweils eine gute Steuerstrategie für jeden Monat berechnet. Jede dieser Steuerstrategien besteht aus einem kompletten Tagesgang der Steuergrößen Heizung, Lüftung und Kohlendioxidzufuhr. Für die Initialisierung der Anfangspopulation werden nicht nur die Steuerstrategie des aktuellen Monats verwendet, sondern auch die Strategien der zwei vorhergehenden und der zwei folgenden Monate. Die Überlegung dabei ist, daß dadurch auch Strategien für kühlere bzw. wärmere Tage im Vergleich zum Durchschnitt des aktuellen Monats in die Initialisierung aufgenommen werden. Außerdem werden neben der reinen Verwendung dieser Strategien weitere Strategien gebildet, indem die Werte der einzelnen Steuergrößen zwischen den Monaten ausgetauscht werden. Am Ende werden alle Vorgaben in einem geringen Maß verrauscht.
Mit dieser Initialisierung konnten sehr gute Erfahrungen gesammelt werden. Meistens ist eine der in der Anfangspopulation enthaltenen Strategien schon recht gut, zumindest werden viele der Beschränkungen eingehalten. Für den Optimierungsalgorithmus steht ,,nur" noch die Aufgabe, in der näheren Umgebung dieser Lösung nach besseren Varianten zu suchen. Wenn in der Anfangspopulation noch keine sehr gute Lösung enthalten ist, so sind in dieser doch viele sinnvolle Elemente enthalten, die durch den Evolutionären Algorithmus innerhalb einiger Generationen zu einem sehr guten Ergebnis kombiniert werden.
Ein weiterer Bereich der Verwendung problemspezifischen Wissens ist die Beschränkung des möglichen Wertebereiches der Steuervariablen in Abhängigkeit des Monats und der Tageszeit. Aus den Ergebnissen von Optimierungen und aus der Praxis wurden für jede Stunde eines Tages in jedem der zwölf Monate ein Maximal- und ein Minimalwert für jede der drei Steuervariablen definiert. Dies bedeutet z.B., daß im Winter die Lüftung einen deutlich kleineren Maximalwert hat als im Sommer, dasselbe gilt für die Nacht. Im Sommer ist dafür der Maximalwert der Heizung kleiner als im Winter. Ähnliche Unterschiede wurden zwischen Tag und Nacht festgelegt.
Bei der Festlegung von Beschränkungen für die Steuervariablen muß beachtet werden, daß dadurch der Suchraum für die Optimierung nicht so stark eingeschränkt wird, daß eine Einhaltung der Beschränkungen der Gewächshausklimagrößen nicht mehr möglich ist. Beispiele dafür sind ein sehr kühler Tag im Sommer, ein sehr sonnenreicher Tag im Frühjahr bzw. eine sehr kalte Nacht im Herbst.
Unter Verwendung des in diesem Unterabschnitt vorgestellten problemspezifischen Vorwissens konnte die Suche nach Lösungen wesentlich robuster durchgeführt und stark beschleunigt werden. Dies zeigte sich insbesondere bei den unter Verwendung realer Wetterdaten durchgeführten Optimierungen.
7.1.5 Ergebnisse: Optimale Steuerung für durchschnittliche Tage |
Dieser Unterabschnitt zeigt die Ergebnisse der Optimierungen des integrierten Gewächshausklimamodells für durchschnittliche Tage im April und Juni. Für die Berechnung des Gewinns wurden die Preise aus Tabelle A3-1, S., benutzt. Abweichend zu den in Unterabschnitt A.3.4, S., aufgeführten Beschränkungen, wurde in diesem Unterabschnitt mit einer maximalen Temperatur im Gewächshaus von 24°C gearbeitet.
Die verwendeten meteorologischen Wetterdaten in diesem und dem nächsten Unterabschnitt sind Durchschnittswerte über 10 Jahre für Potsdam/Deutschland. Deshalb sind diese Daten glatt und ohne Störungen. Die Blattfläche pro Quadratmeter ist im Februar am kleinsten (0,5m2/m2) und im Juni am größten (2,5m2/m2).
Das jeweils linke Diagramm der Abbildungen 7-4 - 7-7 zeigt die Verläufe der Zustandsvariablen des Gewächshauses: Luftfeuchtigkeit, DDI, Gleichung A3-2, Temperatur, TEMI, Gleichung A3-1, und CO2-Konzentration, CI, Gleichung A3-3. Die CO2-Konzentration wurde zur Skalierung auf den Wertebereich der anderen beiden Variablen durch 100 dividiert. Die Verläufe von Biomasse, BIOM, und Gewinn, GEWI, Gleichung A3-6, sind jeweils im mittleren Diagramm der oben genannten Abbildungen dargestellt (summiert über die Zeit - cumulative sum). Die Biomasse wurde durch 100 dividiert, um mit dem Gewinn in einem Diagramm dargestellt werden zu können. Das jeweils rechte Diagramm zeigt die Verläufe der 3 Stellgrößen: Heizung, Q, Lüftung, LR und CO2-Zufuhr, W, wobei die Werte der CO2-Zufuhr mit 10 multipliziert wurden.
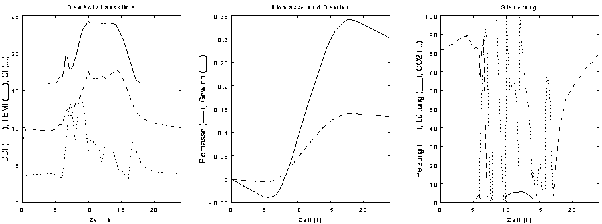
Abbildung 7-4: Ergebnisse der Optimierung durchschnittlicher Tage für den Monat April
Im April, Abbildung 7-4, ist die Heizung die gesamte Nacht an. Dadurch wird die Einhaltung der unteren Temperaturschwelle von 16°C gesichert. Während des Tages ist die Heizung nicht notwendig. Die Lüftung wird nur über die Mittagszeit in geringem Maße benutzt, wodurch die Temperatur unter der oberen Schwelle von 24°C gehalten wird. Da die Lüftung den gesamten Tag über recht gering oder ausgeschaltet ist, wird ständig Kohlendioxid zugeführt, wodurch die CO2-Konzentration tagsüber hoch gehalten wird.
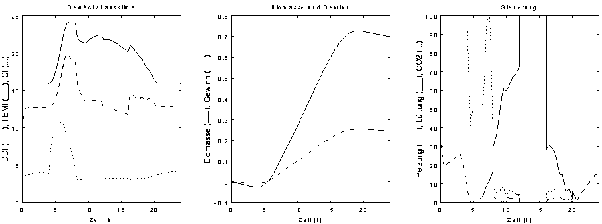
Abbildung 7-5: Ergebnisse der Optimierung durchschnittlicher Tage für den Monat Juni
Im Juni, Abbildung 7-5, ist das Ergebnis ein ganz anderes. Die Lüftung ist den gesamten Tag an, um die Temperatur niedrig zu halten. Am Morgen, wenn die Lüftung noch ausgeschaltet ist, aber die Sonne bereits scheint (Sonnenaufgang etwa gegen 4 Uhr), wird Kohlendioxid zugeführt, um die CO2-Konzentration zu erhöhen. Dies führt zu einer stärkeren Biomasseproduktion. Sobald die Lüftung zur Einhaltung der oberen Temperaturschwelle geöffnet wird, ist CO2-Anreicherung nicht länger sinnvoll. Die Heizung wird nur während der Nacht in geringem Maße benutzt, damit die untere Temperaturschwelle von 16°C eingehalten wird.
7.1.6 Ergebnisse: Optimale Steuerung bei veränderten Preisen |
Dieser Unterabschnitt zeigt die Ergebnisse von Optimierungen, bei denen im Vergleich zum vorigen Abschnitt veränderte Preise zugrunde gelegt wurden. Für die folgenden Berechnungen wurde der Preis für Heizung (Energie) und die CO2-Zufuhr gegenüber dem Standardpreis verändert. Abhängig von der Größe der Änderung kann sich der Verlauf der Stell- und Zustandsgrößen nur etwas oder stark verändern. Da die verwendeten Wetterdaten Durchschnittswerte und damit glatt und ohne Störungen sind, wurden hier zwei drastische Änderungen der Preise eingesetzt, um die Auswirkungen zeigen zu können.
Bei den in Abbildung 7-6 gezeigten Ergebnissen waren der Energie- und Kohlendioxidpreis 3 mal so hoch wie der Standardpreis aus Tabelle A3-1. Im Ergebnis ist die Heizung so gering wie möglich, um trotzdem noch die untere Temperaturbeschränkung einzuhalten. Während des Tages wird so gut wie kein Kohlendioxid zugeführt, die Lüftung wird nie eingeschaltet.
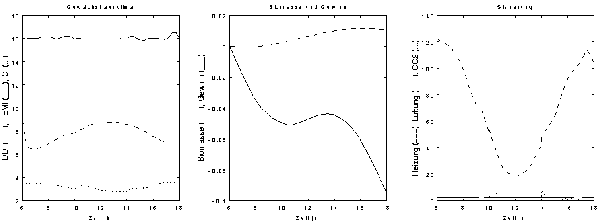
Abbildung 7-6: Ergebnisse der Optimierung durchschnittlicher Tage für den Monat Februar unter Zugrundelegung eines hohen Energie- und Kohlendioxidpreises
Unter Zugrundelegung eines niedrigen Energie- und Kohlendioxidpreises (1/3 des Standardpreises aus Tabelle A3-1), Abbildung 7-7, ergibt sich ein anderes Bild. Hier ist die Heizung höher, als es die Einhaltung der unteren Temperaturbeschränkung erfordert. Zusätzlich wird während des Tages Kohlendioxid zugeführt. Die im Verlauf des Tages produzierte Biomasse (BIOM=1,5 g/m2) ist höher, verglichen mit der unter erhöhten Preisen erreichten Biomasseproduktion (BIOM=1,1 g/m2). Durch die niedrigeren Preise ist der Gewinn viel größer und positiv.
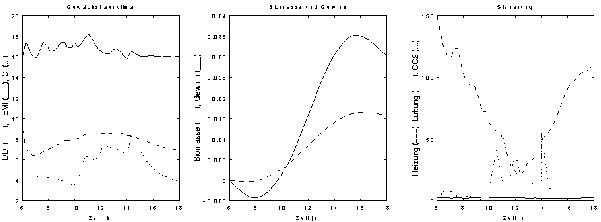
Abbildung 7-7: Ergebnisse der Optimierung durchschnittlicher Tage für den Monat Februar unter Zugrundelegung eines niedrigen Energie- und Kohlendioxidpreises
7.1.7 Ergebnisse: Optimale Steuerung unter Verwendung realer Wetterdaten |
Dieser Unterabschnitt zeigt eine Auswahl der Ergebnisse von Optimierungen des integrierten Gewächshausklimamodells unter Verwendung realer Wetterdaten des Jahres 1995 in Großbeeren bei Berlin. Für die Berechnung des Gewinns wurden die Preise aus Tabelle A3-1, S., benutzt.
Die Darstellung der Ergebnisse weicht etwas von der in den vorigen Unterabschnitten ab. Einmal werden Ergebnisse für jeweils mehr als einen Tag in einer Grafik dargestellt. Außerdem enthalten die Abbildungen zusätzlich eine Grafik mit den verwendeten Klimagrößen. Dadurch ist schnell zu erkennen, worin die Ursachen bestimmter Steuerstrategien liegen. Alle Grafiken enthalten Legenden, die zusätzlich zu den Namen der Größen die teilweise verwendeten Skalierungsfaktoren der einzelnen Größen enthalten. Die Zeitachse aller Grafiken bezieht sich auf den entsprechend fortlaufend numerierten Tag des Jahres.
Die Optimierung des integrierten Gewächshausklimamodells wurde für den Zeitraum April - September 1995 durchgeführt. Die folgenden Abbildungen enthalten Ausschnitte aus diesem Zeitraum. Es wurden solche Gruppen von aufeinanderfolgenden Tagen ausgewählt, die typisch für den entsprechenden Monat sind bzw. in denen auf Grund von Wetteränderungen deutlich unterschiedliche Steuerstrategien innerhalb der einzelnen Tage zur Anwendung kamen.
Der für den Monat April in Abbildung 7-8 dargestellte Zeitraum umfaßt fünf Tage. Das Klima dieser Tage unterscheidet sich am stärksten in der gemessenen Globalstrahlung. Am ersten Tag ist die Globalstrahlung im mittleren Bereich. Die folgenden beiden Tage wurde eine wesentlich geringere Globalstrahlung gemessen. An den letzten beiden Tagen dagegen war die Globalstrahlung sehr hoch, wobei der Wert am fünften Tag noch höher als am vierten Tag war. Entsprechend dieser Unterteilung lassen sich unterschiedliche Verläufe für die Steuer- und Klimagrößen beobachten.
Abbildung 7-8: Ergebnisse der Optimierung unter Verwendung realer Wetterdaten für einige Tage im April
An den ersten vier Tagen wird tagsüber keine Lüftung benötigt. Dadurch kann durch Kohlendioxidzufuhr die Kohlendioxidkonzentration im Gewächshaus erhöht werden. In der linken oberen Grafik ist deutlich die Zunahme der Kohlendioxidkonzentration tagsüber für diese Tage zu erkennen. Am fünften Tag sieht die Steuerung und damit der Verlauf der Klimagrößen deutlich anders aus. Ab dem frühen Morgen wird die Lüftung benutzt, ab Mittag ist die obere Beschränkung der Lüftungsrate erreicht. Eine Anreicherung mit Kohlendioxid wird nicht vorgenommen, da durch die hohe Lüftungsrate eine Erhöhung der Kohlendioxidkonzentration zu teuer ist.
An allen Tagen muß nachts geheizt werden, um den vorgegebenen Minimalwert der Innentemperatur nicht zu unterschreiten. Am zweiten und dritten Tag muß allerdings auch tagsüber weiter, wenn auch deutlich weniger, geheizt werden, um die untere Temperaturschranke einzuhalten.
Die erhöhte Biomasseproduktion an den Tagen mit höherer Globalstrahlung ist in der rechten oberen Grafik zu erkennen. Da zusätzlich weniger geheizt werden muß, wird der Gewinn noch weiter erhöht. Besonders deutlich ist dies am fünften Tag zu erkennen.
Abbildung 7-9: Ergebnisse der Optimierung unter Verwendung realer Wetterdaten für einige Tage im Mai
Die Ergebnisse der ausgewählten Tage im Monat Mai sind in Abbildung 7-9 dargestellt. Besonders interessant für diese Periode ist der dritte Tag. An diesem Tag war die Globalstrahlung gering. Entsprechend groß waren die Auswirkungen auf die Steuerstrategie, die für diesen Tag berechnet wurde. Über den gesamten Tag mußte geheizt werden, um die untere Temperaturschwelle im Gewächshaus zu halten. Weiterhin ist zu sehen, daß nur in der Zeit Kohlendioxid zugeführt wird, in der auch Globalstrahlung vorhanden war, ein erkennbar kürzerer Zeitraum, als an den anderen Tagen. In der kurzen Zeit, in der ausreichend Globalstrahlung für eine Zunahme der Biomasse vorhanden war, konnte allerdings nicht so viel Biomasse produziert werden, wie über Nacht wieder verbraucht wurde. In der rechten oberen Grafik ist zu erkennen, daß es am dritten Tag zu einer deutlichen Verringerung der Biomasse kam.
Abbildung 7-10 enthält die Ergebnisse für Tage des Monats Juni. Bei einem ersten Blick auf den Verlauf der Biomassezunahme und des Gewinns, rechte obere Grafik, sehen alle fünf Tage sehr ähnlich aus. Ein Blick auf die anderen Grafiken zeigt aber, daß dies nicht so ist. Am zweiten und dritten Tag ist die Globalstrahlung geringer, als an den anderen Tagen. Es wird keine Lüftung benötigt, wodurch wiederum Kohlendioxid zugeführt werden kann. An den anderen Tagen wird nur in der Zeit am Morgen Kohlendioxid zugeführt, in der die Lüftung noch nicht geöffnet ist. Die geringeren Außentemperaturen haben für die Nächte zum zweiten, dritten und vierten Tag zur Folge, daß geheizt werden muß.
Abbildung 7-10: Ergebnisse der Optimierung unter Verwendung realer Wetterdaten für einige Tage im Juni
Die in diesem Unterabschnitt gezeigten Ergebnisse der Optimierung mit dem Gewächshausklimamodell unter Verwendung realer Klimadaten zeigen die direkte Reaktion der Steuergrößen auf sich verändernde Klimagrößen. Auf den ersten Blick nicht sehr groß erscheinende Unterschiede in den klimatischen Bedingungen verschiedener Tage können zu deutlichen Unterschieden in den berechneten Steuerstrategien führen. Ein Beispiel dafür ist der Unterschied der Steuerstrategien für den vierten und fünften Tag der dargestellten Tage im April, Abbildung 7-8. Am fünften Tag sind die Globalstrahlung und die Außentemperatur höher als an den anderen Tagen im April. Dadurch muß die Lüftung verwendet werden, eine Kohlendioxidzufuhr macht keinen Sinn. Trotz der höheren Globalstrahlung am fünften Tag ist die Biomasseproduktion am vierten Tag auf Grund der höheren Kohlendioxidkonzentration höher. Ähnliche Beispiele lassen sich an verschiedenen anderen Stellen finden.
In den Erläuterungen dieses Unterabschnitts wurde nur auf einige der Abhängigkeiten bzw. erklärenden Ursachen für bestimmte Steuerungen oder Effekte eingegangen. Bei der Optimierung und Simulation des Modells werden viele weitere Abhängigkeiten einbezogen, die sich in den Grafiken oftmals nicht so einfach ablesen lassen. Die hier dargestellten Ausschnitte aus einer mehrere Monate umfassenden Optimierung der Steuerung zeigen die Funktionsweise des verwendeten Gewächshausklimamodells und der Optimierungsmethode bei der Verwendung realer Wetterdaten.
7.1.8 Zusammenfassung und Ausblick |
Die in diesem Abschnitt vorgestellte Optimierung der Steuerung des Gewächshausklimas verwendet einen anderen Ansatz als viele andere Arbeiten auf dem Gebiet der Gewächshausklimatisierung. Es wird nicht, wie sonst üblich, nach der besten Reglereinstellung bzw. -vorgabe für Temperatur und Kohlendioxidkonzentration im Gewächshaus gesucht. Statt dessen werden direkt die Steuergrößen Heizung, Lüftung und Kohlendioxidzufuhr optimiert. Durch diese direkte Beeinflussung des Gewächshausklimas ist eine vollständige Steuerung aller beeinflußbaren Zustandsgrößen möglich. Außerdem ist durch das Kurzfristmodell eine detaillierte Steuerung und damit Beeinflussung der Zustandsgrößen erreichbar.
Die ermittelten Steuerstrategien für Heizung, Lüftung und CO2-Anreicherung zur Einstellung optimaler Klimazustände im Gewächshaus in Abhängigkeit von der Jahreszeit und den Preisen stehen im Einklang mit der Erfahrung und theoretischen Erkenntnissen. Die Einsatzfähigkeit der vorgestellten Optimierungsmethode zeigen insbesondere die Szenarienrechnungen mit realen Wetterdaten, die sich über einen großen Teil einer Vegetationsperiode ausdehnen. Die dargestellten Ausschnitte zeigen nur einzelne Tage bzw. Wochen, die charakteristisch für längere Perioden sind bzw. Extremwerte darstellen. Die Optimierung wurde für die Monate April bis September komplett durchgeführt.
Eine Weiterentwicklung der zugrunde gelegten Optimierungsmethode und die gezielte Anwendung auf spezifische Aufgaben der Gewächshausklimasteuerung ist somit gerechtfertigt. Für eine Online-Optimierung muß weiter versucht werden, die gegenwärtigen Rechenzeiten (15-30 Minuten für ein Optimierungsintervall von 4 Stunden) zu reduzieren. Möglichkeiten dazu werden u.a. in der weiteren Einbeziehung problemspezifischen Wissens und in der Weiterentwicklung der Algorithmen, z.B. durch Entwicklung problemspezifischer Rekombinations- und Mutationsoperatoren, gesehen.
Ein nächster Schritt der Anwendung der hier vorgestellten und optimierten Steuerung des Gewächshausklimas ist die Einbeziehung verschiedener Strategien zur Vorgabe unterschiedlicher Optimalitätskriterien und Beschränkungen, z.B. durch Einbeziehung übergeordneter Langfristmodelle des Wachstums. Diese Kopplung von Langfristmodellen mit Kurzfristmodellen stellt eine notwendige Voraussetzung für den späteren praktischen Einsatz einer solchen Steuerung dar. Als Langfristmodelle können z.B. die in den Arbeiten von Arnold [Arn87], Markert [Mar90] und Schmidt [Sch85] verwendeten Modelle und optimierten Steuerstrategien zum Einsatz kommen. Die Kopplung zwischen den Lang- und Kurzfristmodellen ist aber nicht so einfach. Eine offene Frage ist die Definition der Zielkriterien und welches Modell bzw. welche Optimierung welche Kriterien behandelt.
Die Kopplung von Modellen unterschiedlicher Abstraktionsebenen (Lang-, Mittel- und Kurzfristmodell) wurde von Alscher in [Als93] vorgestellt. Sie verwendete ein Phasenmodell SAPHASE (Langfristmodell) für die Berechnung der Steuerstrategien über eine Wachstumsphase. Diesem war ein Tagesmodell SATAG nachgeordnet, das zur Bestimmung der Steuerstrategie eines Tages diente. Das Tagesmodell wurde mit einem Stundenmodell SASTUNDE (Kurzfristmodell) unterbaut, das die Steuerstrategien für die stündliche kurzfristige Steuerung berechnet. Es war ein zusätzliches Kopplungsmodell SAKOPPEL notwendig, das die voneinander abweichenden Vorhersageergebnisse der einzelnen Modelle miteinander koppelt und zu einer einheitlichen Bewertung führt. Eine Optimierung fand unter Anwendung der Simulationsmethode statt. Damit wurden die Ergebnisse aller Kombinationen einer Anzahl von vorgegebenen Reglereinstellungen durch Simulation der Modelle ermittelt und die Kombination der Reglereinstellungen mit dem besten Ergebnis (direkt- und flächenkostenfreie Leistung) als optimale Lösung verwendet. Eine zeitabhängige Veränderung der Reglereinstellung über den Simulationszeitraum war nicht vorgesehen, für jedes der Modelle wurde mit einer konstanten Reglereinstellung gearbeitet.
Das Problem der im allgemeinen im voraus nicht ausreichend genau bekannten Klimagrößen läßt sich durch Klimavoraussagen und die Anwendung der repetierenden Optimierung lösen. Mit einer langfristigen Klimavorhersage (ein bis mehrere Tage) wird eine erste Optimierung durchgeführt. Diese dient als Grundlage für weitere Optimierungen, die auf einer kurzfristigeren Wettervorhersage basieren. Je nach Güte der Wettervorhersage kann damit eine ausreichende Übereinstimmung zwischen den mit der berechneten optimalen Steuerung einzustellenden Zustandsgrößen und den tatsächlich gemessenen Zustandsgrößen erreicht werden. Bei immer noch zu großen Abweichungen muß in einer Wiederholung der Optimierung eine weitere Verkürzung des Vorhersagezeitraumes unternommen werden.
Die in dieser Arbeit verwendete spezielle Initialisierung kann als eine repetierende Optimierung angesehen werden. Die Daten für die Initialisierung stammen aus einer Optimierung der Gewächshaussteuerung unter Verwendung von Klimadaten durchschnittlicher Tage dieser Jahreszeit bzw. des entsprechenden Monats. In der nachfolgenden Optimierung unter Verwendung realer Klimadaten wurden die Ergebnisse der ersten Optimierung für die Initialisierung genutzt. Diese nachfolgende Optimierung mußte ,,nur" noch die Anpassung auf die veränderten Klimagrößen vornehmen.
Eine repetierende Optimierung wurde in den Arbeiten von Arnold [Arn87] und Markert [Mar90] bei der Anwendung einer Langfriststeuerung vorgestellt und verwendet. Auch Alscher verwendete in [Als93] eine repetierende Optimierung.
Durch eine weitere Verbesserung und Erweiterung der Pflanzenmodelle (CO2-Gaswechsel, Transpiration, Wachstum) und des Gewächshausmodells kann die Genauigkeit der Vorhersagen weiter verbessert werden. Dies würde einen erweiterten und verbesserten Einsatz der Modelle ermöglichen.
Diese Dokument ist Teil der Dissertation von Hartmut Pohlheim
"Entwicklung und systemtechnische Anwendung Evolutionärer Algorithmen".
This document is part of the .
The is not free.
© Hartmut Pohlheim, All Rights Reserved,
(hartmut@pohlheim.com).