3.3 Rekombination
3.3 Rekombination |
|
Durch die Rekombination werden aus zwei oder mehr Elternindividuen die Nachkommen gebildet. Dies geschieht durch Kombination der Variablenwerte der Eltern. In Abhängigkeit der Repräsentation kommen verschiedene Verfahren zum Einsatz.
Im ersten Unterabschnitt wird die diskrete Rekombination erläutert, die sich auf alle Repräsentationen von Variablen anwenden läßt. Im zweiten Unterabschnitt werden Verfahren speziell für reelle Variablen vorgestellt und im dritten Unterabschnitt für binäre Variablen.
Verfahren für ganzzahlige Variablen lassen sich aus den Verfahren für reelle Variablen ableiten. Die Verfahren für binäre Variablen, die alle eingeschränkte Spezialfälle der diskreten Rekombination sind, lassen sich natürlich auch für reelle und ganzzahlige Variablen verwenden.
3.3.1 Diskrete Rekombination |
|
Diskrete Rekombination [MSV93a] führt einen Austausch der Variablen zwischen den Elterindividuen zur Bildung der Nachkommen durch. Für jede Variablenposition wird entschieden, von welchem Elter der Variablenwert verwendet wird.
(3-15)
Die diskrete Rekombination kann Nachkommen auf den Eckpunkten eines Hyperwürfels erzeugen, der durch die Variablenwerte der Eltern aufgespannt wird. Eine deutsche Benennung als Eck-Rekombination würde deutlicher die Funktionsweise zum Ausdruck bringen. Abbildung 3-12 zeigt diesen geometrischen Effekt der diskreten Rekombination.
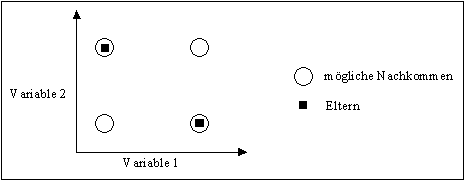
Abbildung 3-12: Mögliche Positionen der Nachkommen nach einer diskreten Rekombination in Bezug auf die Position der Eltern
Eine Erweiterung der hier beschriebenen diskreten Rekombination mit zwei Eltern auf die Verwendung einer höheren Anzahl von Eltern ist offensichtlich. Für jede Variablenposition wird die Variable des Nachkommen von einem der Eltern ausgewählt, wobei alle Eltern dieselbe Wahrscheinlichkeit haben, Variablen zu einem Nachkommen beizusteuern.
Diskrete Rekombination kann auf alle Repräsentationen der Variablen (reell, ganzzahlig, binär, Symbole) angewendet werden.
3.3.2 Rekombination reeller Variablen |
|
Die in diesem Unterabschnitt beschriebenen Rekombinationsverfahren können bei der Rekombination von Individuen mit reellen Variablen Anwendung finden.
Intermediäre Rekombination (intermediate recombination) [MSV93a] kombiniert die Variablen der Eltern nach dem folgenden Verfahren:
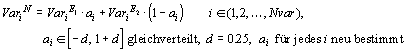(3-16)
Der Skalierungsfaktor a wird gleichverteilt im Intervall [-d, 1+d] für jede Variable neu gewählt. Mit der Größe des Wertes d wird festgelegt, wie groß der Bereich ist, in dem die Variablen der Nachkommen liegen können. Für einen Wert von d = 0 ist der mögliche Bereich der Nachkommen genau so groß wie der Bereich, der von den Eltern aufgespannt wird. Da die meisten Variablen der Nachkommen aber nicht auf den Grenzen des Bereiches liegen, kommt es allein durch die Anwendung der intermediären Rekombination zu einer schrittweisen Verkleinerung des Variablenbereiches. Dies kann durch ein größeres Intervall für den Wert von a verhindert werden. Mit einem Wert von d = 0.25 wird erreicht, daß der Bereich, der durch die erzeugten Nachkommen aufgespannt wird (über viele Versuche gesehen), genau so groß ist, wie der Bereich der Eltern.
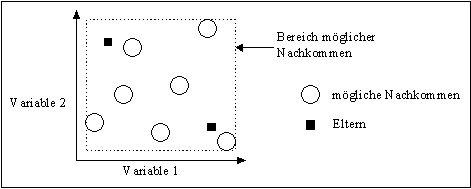
Abbildung 3-13: Mögliche Positionen der Nachkommen nach einer intermediären Rekombination in Bezug auf die Position der Eltern
Die intermediäre Rekombination kann Nachkommen in einem Hyperwürfel erzeugen, der etwas größer ist, als der durch die Variablenwerte der Eltern aufgespannte Hyperwürfel. Wieviel größer der Hyperwürfel der Nachkommen ist, hängt vom Wert des Parameters d ab. Eine deutsche Benennung als Raum-Rekombination würde deutlicher die Funktionsweise zum Ausdruck bringen. Abbildung 3-13 veranschaulicht diesen geometrischen Effekt der intermediären Rekombination.
Linien-Rekombination [MSV93a] ist der intermediären Rekombination ähnlich. Im Unterschied zur intermediären Rekombination wird bei der Linien-Rekombination nur ein und derselbe Skalierungsfaktor a für alle Variablen verwendet, um den Anteil der Variablenwerte der beiden Eltern zu bestimmen.
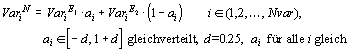(3-17)
Für daß Intervall, in dem a gleichverteilt ausgewählt wird, gelten die gleichen Aussagen, wie für die intermediäre Rekombination.
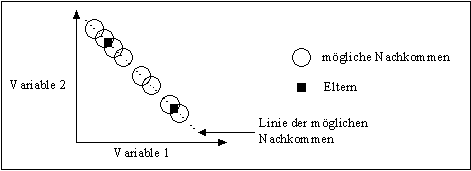
Abbildung 3-14: Mögliche Positionen der Nachkommen nach einer Linien-Rekombination in Bezug auf die Position der Eltern
Linien-Rekombination kann Nachkommen auf einer Linie generieren, die durch die Variablenwerte der Eltern festgelegt wird. Die Nachkommen können nicht nur auf der Strecke zwischen den Eltern liegen, sondern auch außerhalb der Strecke zwischen den Eltern. Wie bei der intermediären Rekombination wird die Länge dieser Strecke durch den Wert von d festgelegt. In Abbildung 3-14 wird dieser geometrische Effekt in zwei Dimensionen dargestellt.
Ein Spezialfall der Linien-Rekombination (und damit auch der intermediären Rekombination) ist die Mittelwertrekombination. Bei dieser wird der Wert von a gleich 0.5 gesetzt. Die Variablen der Nachkommen bilden durch diese Festlegung von a die Mittelwerte der Variablen der Eltern. In Abbildung 3-14 würden die Nachkommen dadurch genau in der Mitte zwischen den Eltern liegen. Durch die eindeutige Festlegung von a fehlt bei der Mittelwertrekombination das stochastische Element. Statt dessen handelt es sich um einen deterministischen Operator, eben die Mittelwertbildung. Verwendet wird dieser Operator im Bereich der Evolutionsstrategien zur Rekombination der Strategieparameter (Größe der Mutationsschrittweiten) und wird dort als intermediäre Rekombination bezeichnet.
Die erweiterte Linien-Rekombination [Müh94] erzeugt die Nachkommen auf einer Linie, die durch die Variablenwerte der Eltern festgelegt wird. Im Gegensatz zur Linien-Rekombination beschränkt sich die erweiterte Linien-Rekombination nicht auf eine Strecke, die zwischen den Eltern sowie ein Stück außerhalb liegt. Bei der erweiterten Linien-Rekombination definieren die Eltern nur die Linie, auf der Nachkommen erzeugt werden können. Die Länge des Bereiches, in dem die möglichen Nachkommen liegen können, wird in Abhängigkeit des Definitionsbereichs der jeweiligen Variablen festgelegt. In diesem Bereich werden die Nachkommen nicht gleichverteilt erzeugt, sondern Nachkommen werden mit einer hohen Wahrscheinlichkeit in der Nähe und nur mit einer geringen Wahrscheinlichkeit weit entfernt vom ersten Elter erzeugt. Wenn die Fitneß der Eltern verfügbar ist, kann diese Information dazu benutzt werden, daß die Nachkommen um den besseren Elter erzeugt werden. Außerdem ist es möglich, Nachkommen öfters in der Richtung vom schlechteren zum besseren Elter zu erzeugen (gerichtete Rekombination).
Die erweiterte Linien-Rekombination benutzt zur Berechnung der Variablenwerte der Nachkommen das folgende Schema:
(3-18)
Die erweiterte Linien-Rekombination benutzt dasselbe Schema zur Festlegung der Schrittweite, das von der in Unterabschnitt 3.4.1, S., beschriebenen Mutation für reelle Variablen verwendet wird. Der Parameter a bestimmt die relative Schrittweite, durch den Parameter r wird der mögliche Bereich der Schrittweite vorgegeben und der Parameter s bestimmt die Richtung, in die der Rekombinationsschritt durchgeführt wird.
Abbildung 3-15 unternimmt den Versuch der Darstellung des Effekts der erweiterten Linien-Rekombination.
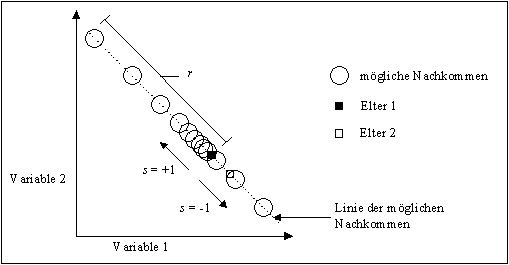
Abbildung 3-15: Mögliche Positionen der Nachkommen nach einer erweiterten Linien-Rekombination in Bezug auf die Position der Eltern und den Definitionsbereich der Variablen
Der Parameter k bei der Berechnung von a bestimmt die Präzision, mit der Schritte erzeugt werden können. Je größer k ist, um so kleinere Schritte können erzeugt werden. Für alle Werte von k ist der maximale Wert von a = 1 (u = 0). Der minimale Wert von a ist abhängig von k und beträgt a =2-k (u = 1). Typische Werte für den Präzisionsparameter k liegen im Bereich von 4 bis 20.
Die Festlegung des Parameters r mit 10% des Definitionsbereiches der Variablen sollte als robuster Startwert verstanden werden. Je nach Art der angegebenen Definitionsbereiche der Variablen sollte eine Anpassung dieses Parameters an die Aufgabenstellung erfolgen. Außerdem kann durch Verkleinerung dieses Parameters während eines Laufs die Suche weiter eingeschränkt werden.
Wenn der Parameter s mit gleicher Wahrscheinlichkeit -1 oder +1 sein kann, dann findet keine gerichtete Erzeugung von Nachkommen statt. Wird s dagegen mit einer höheren Wahrscheinlichkeit zu +1 gesetzt, so werden die Nachkommen öfters in Richtung vom schlechteren zum besseren Elter erzeugt (vorausgesetzt, daß der erste Elter der bessere Elter ist).
Die in diesem Unterabschnitt vorgestellten Verfahren zur Rekombination von Individuen mit reellen Variablen lassen sich ohne Probleme auch auf die Rekombination von Individuen mit ganzzahligen Variablen übertragen. Bei der Berechnung des Skalierungsfaktors bzw. der Schrittweite (Parameter a) muß nur der diskrete Charakter der ganzzahligen Variablen beachtet werden. Der Berechnungsablauf und die Eigenschaften der Verfahren bleiben übertragen erhalten.
3.3.3 Rekombination binärer Variablen (crossover) |
|
Die in diesem Unterabschnitt beschriebenen Rekombinationsverfahren können bei der Rekombination von Individuen mit binären Variablen Anwendung finden. Für die Bezeichnung dieser Verfahren wird im allgemeinen der Begriff crossover verwendet, der deswegen in diesem Unterabschnitt zur Anwendung kommt.
Bei der Rekombination binärer Variablen kommt es nur zu einem Austausch der einzelnen Variablen zwischen den Individuen. Die Verfahren unterscheiden sich darin, in wie viele Stücke die Variablen der Individuen vor dem Austausch zerlegt werden.
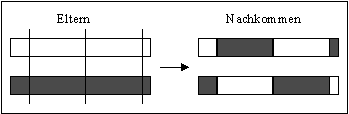
Abbildung 3-16: Ablauf des multi-point crossover
Beim multi-point crossover wird eine Anzahl von Schnittpunkten gleichverteilt zufällig ausgewählt. Die Schnittpunkte werden der Größe nach sortiert. Danach werden die Variablen innerhalb aufeinanderfolgender Schnittpunkte zwischen den Elternindividuen zur Bildung zweier Nachkommen ausgetauscht. Abbildung 3-16 veranschaulicht diesen Prozeß.
Wenn beim multi-point crossover nur eine Schnittposition festgelegt wird, ergibt sich der Spezialfall des single-point crossover. In Abbildung 3-17 ist dieser Vorgang illustriert.
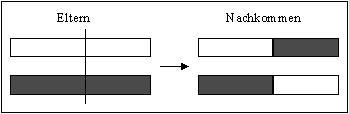
Abbildung 3-17: Ablauf des single-point crossover
Entsprechend kann durch Festlegung von zwei Schnittpunkten double-point crossover durchgeführt werden.
Beim multi-point crossover wurde eine Anzahl von Schnittpunkten festgelegt, zwischen denen die Variablen der Eltern ausgetauscht werden. Uniform crossover [Sys89] erweitert dieses Schema soweit, daß zwischen allen Positionen ein Austausch der Variablen zwischen den Eltern stattfinden kann. Das heißt, für jede einzelne Variable eines Nachkommen wird festgelegt, welcher Elter diese Variable liefert.
Dieses Schema ist identisch zu dem der diskreten Rekombination, die in Unterabschnitt 3.3.1, S., vorgestellt wurde.
Shuffle crossover [CES89] (shuffle (engl.): mischen) ist dem single-point und uniform crossover sehr ähnlich. Vor dem crossover werden die Variablen in beiden Eltern zufällig gemischt. Danach wird ein single-point crossover durchgeführt. Nach dem crossover werden die Variablen wieder auf ihre ursprünglichen Positionen ,,entmischt". Dadurch wird eine Bevorzugung bestimmter Positionen verhindert, da die Variablen vor jedem crossover aufs Neue zufällig gemischt werden.
Der Operator reduced surrogate [Boo87] beschränkt crossover soweit, daß, wenn möglich, neue Individuen produziert werden. Dies wird dadurch erreicht, daß die Positionen der Schnittpunkte auf solche Positionen beschränkt werden, in denen sich die Variablen der Eltern unterscheiden.
Der Grundgedanke hinter multi-point crossover, und auch vielen anderen crossover Varianten, ist, daß die Variablen eines Individuums, die am meisten zur Performanz beitragen, nicht in einem zusammenhängenden Teil eines Individuums enthalten sind [Boo87]. Außerdem wird der auseinanderreißende Effekt des multi-point crossover, im Vergleich zu single-point und double-point crossover, als verstärkte Breitensuche im Suchraum angesehen, anstatt sehr zeitig in der Suche sehr gute Individuen zu bevorzugen. Dadurch soll die Suche robuster werden [SDJ91b].
Uniform crossover, ähnlich wie multi-point crossover, beansprucht, daß die Bevorzugung bestimmter Positionen in Abhängigkeit der Länge der binären Repräsentation und der Kodierung reduziert wird. Dies soll helfen, die Bevorzugung kurzer Variablenketten, wie beim single-point crossover, zu verhindern, ohne ein präzises Verständnis der Wichtigkeit einzelner Variablenpositionen zu benötigen. Spears und De Jong [SDJ91a] haben außerdem gezeigt, wie uniform crossover parametriert wird, indem eine Wahrscheinlichkeit auf den Austausch von Variablen angewendet wird. Dadurch kann der Umfang des ,,Zerreißens" während des crossover unabhängig von der Länge der verwendeten Repräsentation kontrolliert werden.
Diese Dokument ist Teil der Dissertation von Hartmut Pohlheim
"Entwicklung und systemtechnische Anwendung Evolutionärer Algorithmen".
This document is part of the .
The is not free.
© Hartmut Pohlheim, All Rights Reserved,
(hartmut@pohlheim.com).
